Un jeu inéquitable… mais pas dans le sens escompté !

Accepteriez-vous de jouer avec moi au jeu suivant ? Dans la dernière édition du Wall Street Journal, extrayons « au hasard » mille données chiffrées positives, portant sur les cours de bourse, les taux d’intérêt, les taux de change, etc., et ne retenons, pour chaque donnée élémentaire, que son premier chiffre significatif : le premier à gauche, si la donnée est un nombre supérieur à 1, ou le premier chiffre non nul placé après la virgule, si la donnée est comprise entre 0 et 1. Chaque fois que ce premier chiffre significatif est un 1, un 2, ou un 3, vous me payez un euro, et sinon c’est moi qui vous verse un euro. Je vous sens plutôt partant ! Avec six chiffres gagnants en votre faveur, contre seulement trois pour moi, vous pensez sans doute « raisonnablement » gagner dans environ 2/3 des cas, contre seulement 1/3 pour moi, et donc empocher à peu près (2/3 – 1/3) x 1000 = 333 €, après les mille coups de notre partie ! C’est étrange, parce que, de mon côté, j’ai un pressentiment inverse : c’est moi, et non pas vous, qui vais l’emporter en empochant environ 200 €. Vous ne me croyez pas ? Libre à vous et, puisque tel est votre bon vouloir, jouons et nous en aurons le cœur net !

Une heure plus tard… Vous avez perdu 200 € et vous n’en revenez pas ? Vous estimez que j’ai bénéficié d’une chance extraordinaire, défiant toute loi acceptable du hasard ? Eh bien, détrompez-vous : cette issue était parfaitement prévisible et se reproduirait systématiquement, si nous rejouions un très grand nombre de parties, à partir de sources de données très diverses : avec une autre édition du Wall Street Journal ; avec un quelconque journal financier, européen, américain ou japonais, les montants monétaires y étant exprimés en euros, en dollars ou en yens ; ou encore, avec un atlas géographique recensant les longueurs des fleuves et les superficies des lacs ; ou encore, avec un traité d’astronomie empli des masses des étoiles et des distances intergalactiques ; ou encore avec un répertoire d’adresses où figurent des numéros de rues ; ou encore avec un recueil de constantes physiques ; ou encore, avec une recension de capitalisations boursières, un graphe des liens hypertextes pointant vers différents sites, un décompte des amis Facebook ou des volumes de tweets au sein d’un panel d’internautes ; ou enfin, et mieux encore que tout cela, avec une mélange hétéroclite de tous ces registres de données. Un 1, un 2 ou un 3 sortiraient comme premier chiffre significatif dans environ 60 % des cas (et non pas seulement 33 %), si bien que vous me paieriez (60 % – 40 %) x 1000 = 200 €. Surprenant, non ?

Newcomb et Benford

En 1881, l’astronome américain Simon Newcomb publia dans l’American Journal of Mathematics un article qui passa à l’époque presque inaperçu [1]. Il avait remarqué que les recueils de tables de logarithmes étaient nettement plus usés dans leurs premières pages que dans les suivantes. Il en déduisit que les utilisateurs de ces tables, dans les opérations de multiplication qu’ils devaient effectuer, avaient davantage l’occasion de manipuler des nombres dont le premier chiffre significatif est bas que des nombres pour lesquels celui-ci est élevé. Partant de ce constat, Newcomb établit empiriquement la loi de probabilités discrète donnant les fréquences respectives Proba(p) d’apparition des différents chiffres p du système décimal (p = 1, 2,…, 9), comme premier chiffre significatif d’une donnée tirée d’un corpus disparate et sans cohérence apparente. Il obtint ainsi une fonction Proba(p) décroissante selon p, ayant pour expression :

Proba(p) = log_{10}(p + 1) – log_{10} p = log_{10}(1 +1/p)

Presque 60 ans plus tard, en 1938, le physicien Frank Benford [2], qui n’avait pas lu le travail de Newcomb, fait indépendamment le même constat et retrouve à son tour cette même loi empirique, qui restera désormais connue sous le nom de son second découvreur.

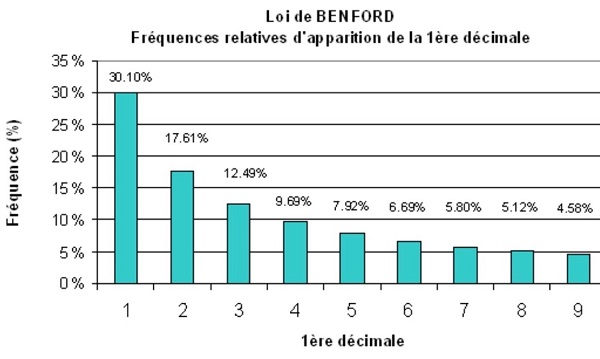
Sur le diagramme ci-dessus, figurant la loi de Benford, on observe notamment que Proba(1) + Proba(2) + Proba(3) ≈ 60 %, d’où ma botte gagnante au jeu que je vous ai si hardiment proposé et que vous avez si promptement accepté.

Pourquoi, de manière si étrange, les plus petits chiffres du système de numération décimale sont-ils de bien meilleurs candidats que les chiffres supérieurs, pour trôner en tant que premier chiffre significatif au sein d’une liste de données erratiques ? Pourquoi, contrairement à l’attente « naturelle », chaque chiffre de 1 à 9 n’a-t-il pas exactement la même probabilité 1/9 d’apparaître ? Pourquoi sommes-nous à ce point victimes d’un biais cognitif privilégiant à tort la loi de distribution uniforme, c’est-à-dire l’équiprobabilité ?

Avant de répondre à ces questions, il convient de mieux circonscrire le domaine de pertinence de la loi de Benford. En effet, celle-ci ne prévaut pas pour tout corpus de données.

Le champ de validité de la loi de Benford

Si, à la différence des contextes jusque là évoqués, le corpus de données, au lieu d’être « déstructuré »,  est au contraire hautement organisé, alors la loi de Benford est mise en défaut. Ainsi, des numéros téléphoniques tirés de l’annuaire de la région sud-est auront tous pour premier chiffre significatif le 4 (04 xx xx xx), sans aucune occurrence possible des huit autres chiffres ! De même les numéros mobiles ne peuvent commencer que par un 6 ou un 7 et les numéros non géographiques via internet, détiennent l’exclusivité du 9 comme premier chiffre significatif. Un violent camouflet à la loi de Benford !

Autres exceptions importantes, les corpus constitués à partir de mesures d’une variable concentrée autour de sa moyenne, comme le poids ou la taille au sein d’une population de référence. Imaginez que je vous propose à nouveau de jouer, les mille données étant cette fois extraites, non pas d’un journal financier, mais du fichier de la Police où sont consignées les tailles des prévenus, exprimées dans le système métrique. Je vous promets cette fois de vous verser un euro chaque fois que le premier chiffre significatif d’une taille sera supérieur à 1, me réservant personnellement le 1 comme unique chiffre gagnant. Acceptez-vous encore de m’affronter ? Je suis convaincu que non, assurés comme vous l’êtes que très peu de prévenus mesuraient moins d’un mètre, ou plus de deux, à la date de leur arrestation. Or il faudrait pourtant quelques nains et géants, pour que vous puissiez gagner ne serait-ce que quelques coups de la partie ! En outre, la distribution statistique du premier chiffre significatif dépend ici du système d’unités : un pic très pointu autour de la valeur 1, dans le système métrique, mais une répartition plus étalée entre les valeurs 3, 4, 5 et 6 dans le système anglo-saxon où la taille est mesurée en pieds !

Les considérations précédentes dessinent en creux le domaine d’application de la loi de Benford. Les deux conditions suivantes doivent être réunies :

  1. le corpus d’où sont extraites les données chiffrées doit être hétérogène et ne pas obéir à un ordre logique prédéterminé ;
  2. ce corpus ne doit pas être concentré autour d’une certaine valeur de référence, mais au contraire étalé sur plusieurs ordres de grandeur

En bref, le royaume de Benford est celui des « bric-à-brac statistiques » !

L’invariance à l’échelle, mère de la loi de Benford

Examinons un « vrai » bric-à-brac, tel celui placé en tête de cet article. À quoi ressemble-t-il ? À rien, me direz-vous sans doute… et c’est même à cela qu’on le reconnaît ! Grave erreur, car un bric-à-brac ressemble bien à quelque chose : il est semblable à toute partie de lui-même, c’est un objet auto-similaire, « invariant à l’échelle » en ce sens que son désordre se répète à toutes les échelles d’observation. Or cette propriété fondamentale d’invariance à l’échelle, très puissante, donne à un apparent bric-à-brac de données une forte structure cachée, induisant en particulier la loi de Benford.

Formulée mathématiquement, l’invariance à l’échelle impose une contrainte à la fonction de répartition des données au sein d’un corpus : si F(x) désigne la proportion de ces données qui sont inférieures à une valeur positive donnée x, alors l’invariance à l’échelle exige que, pour tout facteur multiplicatif k > 0 et pour tout couple (x, y) de valeurs positives telles que y > x, on ait :

F(k.y) – F(k.x)  = F(y) – F(x)

Autrement dit, un corpus de données est invariant à l’échelle si deux intervalles homothétiques l’un de l’autre dans un facteur quelconque ont la même masse.

Par un raisonnement du niveau « classe prépa », on montre que les seules fonctions de répartition vérifiant la condition d’invariance à l’échelle revêtent la forme log-linéaire :

F(x) = a.lnx + b  ,   a > 0

Supposons que le corpus s’étende sur 2N ordres de grandeur du système décimal, chacun du type [10^{n},10^{n+1}]  pour n variant de –N à N – 1. La borne inférieure du support de la distribution est ainsi 10^{-N} et la borne supérieure, 10^{N}. La détermination des constantes a et b découle des conditions aux limites F(10^{-N}) = 0 (aucune donnée n’est inférieure à 10^{-N}) et F(10^{N}) = 1 (aucune donnée du corpus n’est supérieure à 10^{N}). D’où :

F(x) = 1/2 + (1/2N).log_{10} x      ,    10^{-N} \leq x  \leq 10^{N}

Autrement dit, le logarithme en base 10 des données suit une loi uniforme de densité 1/2N sur l’intervalle [–N, N]. Pour cette raison, on dit que la distribution des données au sein d’un corpus invariant à l’échelle est « log-uniforme » (à ne pas confondre avec log-normale).

On remarque que la médiane de la distribution log-uniforme est 1, soit F(1) = 1/2, les N ordres de grandeur inférieurs à l’unité (n = –N, –N+1, …, –1) pesant autant que les N ordres de grandeur supérieurs (n = 0, 1, …, N–1).

Par ailleurs, invariance à l’échelle oblige, les différents ordres de grandeur ont la même masse 1/2N. En outre, au sein de chacun d’eux, la distribution des données est log-uniforme, tout comme elle l’est pour l’ensemble du corpus. En effet, la fonction de répartition F_{n}(x), restreinte  au n^{ème} ordre de grandeur,  s’écrit :

F_{n}(x) = [F(x) – F(10^{n}) ]/[ F(10^{n+1}) – F(10^{n})] = log_{10}x – n  ,  10^{n} \leq x < 10^{n+1}

Cette relation implique que la partie fractionnaire (ou mantisse) du logarithme des données est uniformément distribuée entre 0 et 1, pour chacun des ordres de grandeurs. Ceux-ci apparaissent ainsi comme des copies conformes les uns des autres, autant de réductions pantographiques du corpus global. Mutatis mutandis, l’invariance à l’échelle est à la statistique ce que la texture fractale [3] est à la géométrie, à savoir la propriété d’un objet renfermant des miniaturisations de lui-même.

Venons en maintenant à notre principal point d’intérêt : quelle est la probabilité Proba(p) que le premier chiffre significatif d’une donnée issue d’un corpus invariant à l’échelle soit le chiffre p (p = 1, 2, …, 9) ? En balayant les ordres de grandeur du plus petit au plus grand, on obtient :

Proba(p) = \Sigma{_{n=-N}}^{N-1} {F[(p+1).10^{n+1}] – F[p.10^{n}]}

Proba(p) = 2N.(1/2N).[ log_{10}(p +1) – log_{10} p] = log_{10}(1 +1/p)

Or cette expression n’est autre que la loi de Benford, qui apparaît ainsi comme une conséquence directe de l’invariance à l’échelle.

Une cartographie des corpus statistiques

Dans un essai intitulé Le hasard sauvage, le philosophe Nassim Nicholas Taleb [4] imagine un continent de la statistique séparé en deux contrées : d’un côté, le Mediocristan, où résident les données prisonnières d’un certain ordre de grandeur et convenablement décrites par leur moyenne (medio) et leur écart-type autour de cette moyenne ; d’un autre côté, l’Extrémistan, où résident les données s’étendant sur plusieurs ordres de grandeur et pour lesquelles seule la médiane est un indicateur pertinent, la moyenne étant tirée vers l’infini sous le poids des valeurs extrêmes, selon l’effet dit de longue traîne.

Les corpus de données invariants à l’échelle constituent quant à eux une province de l’Extrémistan, que nous pourrions nommer Similistan en raison de la propriété d’autosimilarité. La loi de Benford est une propriété intrinsèque des corpus du Similistan. Elle demeure toutefois approximativement valable pour des corpus situés dans la région du Mediocristan frontalière du Similistan. En effet, lorsque qu’une loi log-normale, cloche typique dans le paysage du Mediocristan, est très étalée autour de sa moyenne, elle est alors, sur de nombreux ordres de grandeur, proche d’une loi log-uniforme.

Le premier à avoir percé rigoureusement le mystère de la loi de Benford, en 1995, Hill [5], a toutefois quelque peu brouillé les frontières de Taleb, en démontrant qu’une concaténation d’échantillons de données, chacun d’eux étant régi par une loi statistique spécifique et non log-uniforme, engendre un corpus global à peu près invariant à l’échelle, c’est-à-dire obéissant approximativement à la loi log-uniforme.

Quelques résultats complémentaires

La moyenne en fuite

Puisque, dans un corpus invariant à l’échelle, les ordres de grandeur successifs, rangés dans le sens croissant, ont une même masse alors qu’ils sont de plus en plus étendus, il en résulte que la densité F’(x) des données est une fonction homographiquement décroissante le long de la demi-droite des nombre réels positifs, soit :

F’(x) =(1/2N.ln10).(1/x)

En calculant, à l’aide de cette densité, la moyenne \mu et le coefficient de variation CV (ratio rapportant l’écart-type \sigma à la moyenne \mu) de la loi log-uniforme sur le support [10^{-N}, 10^{N}], on obtient aisément :

\mu = (10^{N} – 10^{-N})/2N.ln10    CV = \sigma/\mu = {N.[(10^{N} + 10^{-N})/ (10^{N} – 10^{-N})].ln10}^{1/2}

Ainsi, lorsque le corpus s’étale, c’est-à-dire lorsque le nombre N des ordres de grandeur s’accroît indéfiniment, la moyenne des données « fuit » vers l’avant proportionnellement à 10^{N}/N tandis que le coefficient de variation diverge comme N^{1/2} , ce qui manifeste l’effet de longue traîne propre à l’Extrémistan.

Observation d’un phénomène exponentiel

Il existe de nombreux corpus de données Benford by design, à savoir tous ceux issus de l’observation d’un phénomène dynamique caractérisé par la croissance exponentielle d’une certaine grandeur. Soit en effet r le taux de croissance constant de cette grandeur et [–T, T], la période d’observation. La valeur à l’instant t = 0 étant prise pour unité de mesure, la loi d’évolution a pour expression :

x(t) = exp(r.t)  ,  –T ≤ t ≤ T

Si l’on échantillonne le phénomène à des instants uniformément répartis sur l’intervalle [–T, T], on obtient un corpus de données dont la fonction de répartition s’écrit :

F(x) = Proba[x(t) ≤ x] = Proba[–T ≤ t ≤ (1/r).ln x] = 1/2 + (1/r.T).lnx

On reconnaît ici la loi log-uniforme définie sur 2N ordres de grandeur, où N \approx r.T/2ln10

Cette propriété est très importante, car les séries temporelles engendrées par une variable dont le taux de croissance est approximativement constant sur un très large intervalle de temps, sont très courantes dans l’étude des phénomènes physiques ou économiques.

Invariance à la base de numération

La loi de Benford est valide dans un système de numération de base b quelconque. Supposons en effet que les données d’un corpus invariant à l’échelle soient écrites dans un système numéral de base b quelconque. Les ordres de grandeurs sont alors redéfinis comme les intervalles successifs [b^{n}, b^{n+1}]. Par le même fil de raisonnement que celui suivi pour la base 10, on obtient la loi du premier chiffre significatif (ou symbole significatif si b > 10), soit :

P(p)= log_{b}(1 + 1/p)  ,  p = 1, 2, …b – 1

En écriture binaire, on obtient en particulier P(1) = log_{2} (1 + 1) = log_{2} 2 = 1, ce qui n’est guère étonnant puisque 1 est alors le seul chiffre significatif possible ! Hill [6] a prouvé que la propriété d’invariance à la base suffit seule à caractériser la loi de Benford.

Chiffres significatifs au-delà du premier

Les travaux de Benford ont été généralisés, afin de déterminer les lois régissant l’occurrence d’un chiffre donné comme m^{ème} chiffre significatif. Il apparaît que plus le rang m est élevé, plus la distribution du chiffre significatif figurant à ce rang se rapproche de la distribution uniforme, avec une légère « préférence » persistante au deuxième rang pour l’occurrence des plus petits chiffres ; préférence qui s’évanouit toutefois dès le troisième rang, à partir duquel le « hasard » uniforme, sans structure, sans odeur ni saveur, reprend en définitive ses droits !

À quoi Benford sert-il ?

La loi de Benford a-t-elle des applications pratiques ? La réponse est oui ! Cette loi est en effet précieuse – et effectivement utilisée ! – pour détecter la fraude fiscale, ou le trucage d’une comptabilité, ou encore la malhonnêteté scientifique. L’idée est on ne peut plus simple : si l’on falsifie un corpus de données, alors on déforme artificiellement sa structure statistique, ce qui a pour effet une déviation aux lois log-uniforme et de Benford. Donc, si un vérificateur automatique constate une telle déviation, de deux choses l’une : ou bien la cause de l’écart est clairement identifiable et provient de la nature particulière des données ; ou bien, l’écart est injustifiable de cette manière, les données devraient théoriquement suivre approximativement la loi de Benford, et dans ce cas la suspicion de fraude est forte, un audit approfondi s’impose !

 

Mots-clés : Loi de Benford – biais cognitif d’équiprobabilité – autosimilarité – détection des fraudes.

Références

[1] Newcomb, Simon (1881), Note on the Frequency of Use of the Different Digits in Natural Numbers , American Journal of Mathematics, 4, pp.39-40.

[2] Benford, Frank (1938) The Law of Anonalous Numbers , Proceedings of the American philosophical society, 78, pp.551-572.

[3] Mandelbrot, Benoît (1975), Les objets fractals : forme, hasard et dimension, Flammarion, 190p..

[4] Taleb, Nassim Nicholas (2009), Le hasard sauvage, Les Belles Lettres, 371p.

[5] Hill Theodore P. (1995), Statistical Derivation of the Significant Digit Law, Statistical Science, 10, pp.354-363.

[6] Hill, Theodore P. (1995), Base-Invariance Implies Benford’s Law » Proceedings of the American mathematical society, 123, pp.887-895.

 

Nicolas Curien
Les derniers articles par Nicolas Curien (tout voir)