Nous avons proposé, dans un premier article[1] sur le thème de l’évaluation du niveau des élèves français en mathématiques, une synthèse des résultats issus des enquêtes nationales et internationales d’évaluation des acquis et des compétences des élèves dans cette discipline.
Néanmoins, notre volonté de proposer une vision synthétique des évolutions sur une longue période a nécessairement impliqué de s’en tenir à des indicateurs assez généraux du niveau national en mathématiques (principalement des moyennes nationales et des classements internationaux). Ces indicateurs peuvent parfois s’avérer démesurément simplificateurs, et masquent des réalités plus fines qui sont importantes à relever.
Nous proposons donc dans ce deuxième article de nous appuyer sur notre exploitation des données de l’enquête TIMSS 2019 pour le CM1 et la classe de quatrième afin de caractériser plus précisément le niveau des élèves français en mathématiques et sa distribution.
Nous souhaitons également comparer les performances françaises à celles des élèves d’autres pays de même envergure du point de vue de la production scientifique dans cette discipline (l’Allemagne, l’Angleterre, les Etats-Unis, la Russie, le Japon et Singapour).
Évaluation des acquis et des compétences pour les élèves de Cours Moyen 1.
Pour le CM1, on constate que le score moyen français est significativement inférieur à celui de tous les autres pays étudiés. Le même constat s’impose d’ailleurs pour le niveau des 10, 25, 50, 75 et 90ème percentiles, ce qui signifie que les élèves français sont non seulement moins bons en moyenne, mais également à différents seuils standards de la distribution. On observe par exemple que le niveau du troisième quartile japonais (et a fortiori singapourien) ou de la médiane américaine est supérieur au niveau du premier quartile français.
Nous nous sommes ensuite attachées à comparer entre elles les performances des meilleurs élèves à l’intérieur de chaque pays, et plus précisément les performances des 10, 5 et 1% les meilleurs élèves à l’intérieur du pays[2]. Ceci nous a permis de noter que la moyenne des 1% les meilleurs français n’est pas significativement différente de celle des 1% les meilleurs allemands, mais qu’elle est significativement inférieure à celle des 1% les meilleurs élèves pour tous les autres pays considérés. De même, la moyenne des 5 et 10% des meilleurs français est significativement inférieure à celle des 5 et 10% les meilleurs élèves de tous les autres pays. En somme, l’idée selon laquelle, si les élèves français sont en moyenne moins bons que leurs homologues internationaux, ils sont en revanche meilleurs ou de même niveau en haut de la distribution, est fausse.
On notera également que les meilleurs anglais obtiennent de meilleurs scores que les meilleurs russes, ce qui les place en 3ème position du point de vue des performances des meilleurs élèves alors qu’ils sont en 4ème position du point de vue du score moyen. En d’autres termes, l’hypothèse parfois formulée à tort au sujet de la France (médiocrité moyenne mais excellence en haut de la distribution), serait plutôt vraie dans une certaine mesure pour l’Angleterre.
Nous avons également regardé l’écart entre les résultats obtenus par les meilleurs élèves et le niveau d’ensemble, afin d’avoir une idée de l’ampleur des écarts de niveau au sein de chaque pays. De ce point de vue, les pays se classent dans l’ordre suivant (du plus grand au plus petit écart entre les meilleurs et l’ensemble) : Angleterre, Etats-Unis, France, Singapour, Russie, Japon, Allemagne. Nous avons pu observer par ailleurs qu’entre 2015 et 2019, le groupe des meilleurs 10% français s’est éloigné de l’ensemble. En effet, le niveau de l’ensemble a très légèrement baissé et le niveau des meilleurs 10% s’est très légèrement accru (phénomènes qui, pris isolément, ne sont pas significatifs, mais qui, cumulés, le sont). Il en résulte qu’en 2019 (et c’est une nouveauté par rapport à 2015), les meilleurs français ne sont pas significativement moins éloignés de l’ensemble des français que ne le sont les meilleurs américains de l’ensemble des américains (ou a fortiori les meilleurs anglais de l’ensemble des anglais). En revanche, on voit qu’en 2019, les meilleurs singapouriens, japonais et russes sont significativement plus proches de l’ensemble que ce n’est le cas en France, ce qui n’était pas vrai en 2015 (ce n’était vrai en 2015 que pour l’Allemagne).
Dans le même esprit, nous avons comparé entre elles les moins bonnes performances à l’intérieur de chaque pays. Nous avons, en premier lieu, constaté que les moins bons élèves français sont en moyenne significativement moins bons que les moins bons élèves de tous les autres pays.
En revanche, de manière générale, le classement des pays selon les performances des moins bons élèves est sensiblement différent du classement selon les performances moyennes. En effet, si les moyennes globales permettent de classer les pays dans l’ordre suivant (par ordre croissant de performance) : France, Allemagne, Etats-Unis, Angleterre, Russie, Japon, Singapour, les moyennes sur les groupes de moins bons élèves donnent le classement suivant : France, Etats-Unis, Allemagne/Angleterre, Russie, Japon/Singapour. On voit donc que si l’Angleterre a de très bons meilleurs élèves, elle a aussi de relativement mauvais plus mauvais élèves, et qu’a fortiori, les Etats-Unis ont également de relativement mauvais plus mauvais élèves.
Ceci peut s’expliquer par la distance entre l’ensemble des élèves et les moins bons élèves dans chaque pays : on observe globalement qu’en Angleterre et aux Etats-Unis, les moins bons élèves sont très éloignés de l’ensemble (et les Etats-Unis sont le seul pays pour lequel cet écart croît significativement entre 2015 et 2019). Cet écart est significativement moindre en France. À l’inverse, les moins bons élèves sont plus proches de l’ensemble au Japon, en Allemagne et en Russie qu’en France.
Le graphique suivant permet de résumer les observations précédentes en fournissant une représentation des distributions du niveau estimé des élèves de CM1 en 2019 pour chaque pays[3] :
Densités et boîtes à moustache représentant le score estimé en mathématiques des élèves de CM1 pour tous les pays en 2019
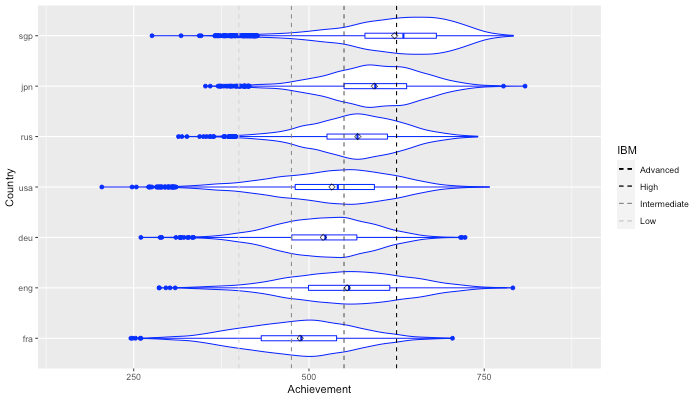
Source : IEA (International Association for the Evaluation of Educational Achievement), TIMSS 2019 Database
Nous avons également étudié les différents seuils de niveau fixés par TIMSS (“Below Low”, “Low”, “Intermediate”, “High”, “Advanced”) pour comparer les différents pays entre eux. Nous avons ainsi pu observer que pour la France, les proportions d’élèves appartenant à chaque seuil de niveau sont significativement différentes des proportions observées dans les autres pays. Ainsi, plus d’élèves, relativement à l’ensemble, se placent dans les niveaux “Below Low”, “Low” et “Intermediate”, et moins d’élèves, relativement à l’ensemble, se classent dans les niveaux “High” et “Advanced”. La seule exception est l’Allemagne qui a une part significativement plus élevée que la France d’élèves de niveau “Intermediate”. Ces résultats sont observables sur le graphique suivant :
Répartition par seuil de performance en mathématiques des élèves de niveau CM1 pour tous les pays
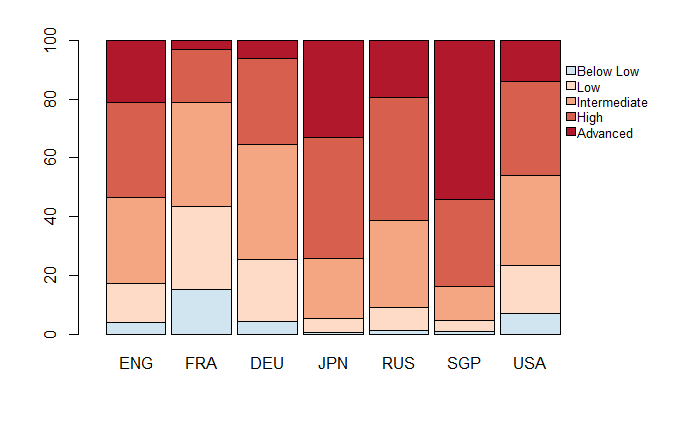
Source : IEA, TIMSS 2019 Database
En somme, nous pouvons conclure que pour le CM1, la France a un niveau bien inférieur à celui des autres pays du groupe étudié.
Elle se distingue surtout par une part importante d’élèves en difficulté, que ne vient pas compenser un groupe important de très bons élèves, ou un petit groupe d’excellent niveau sur un plan international.
La part d’élèves en échec par rapport à un seuil fixe s’accroît, ce qui peut s’expliquer par le fait que les performances des moins bons élèves à l’intérieur du pays sont de moins en moins bonnes. On observe néanmoins un léger décrochage des meilleurs 10% entre 2015 et 2019 par rapport à l’ensemble, qui s’explique par la conjonction d’une hausse très légère du niveau des meilleurs et une hausse très faible du niveau d’ensemble.
Enfin, la France se classe au milieu des pays observés du point de vue de l’écart entre les performances extrêmes et l’ensemble des performances : cet écart est plus important en Angleterre, aux Etats-Unis, il est moins important en Russie, en Allemagne, au Japon et à Singapour.
Évaluation des acquis et des compétences pour les élèves de Quatrième.
Pour la Quatrième, nous avons travaillé sur le même groupe de pays, à l’exception de l’Allemagne qui n’a pas participé à l’enquête pour ce niveau. Comme pour le CM1, on note que la moyenne française est significativement inférieure à celle des autres pays.
On remarque également pour ce niveau de grandes disparités entre les pays dans l’écart-type des scores. Ainsi, les scores français sont bien moins dispersés que ceux des autres pays, et les scores américains le sont bien plus. L’importante dispersion des scores américains et, dans une moindre mesure, des scores anglais, peut permettre d’expliquer que le niveau du premier décile n’est pas significativement plus élevé pour ces deux pays que le niveau du premier décile français, malgré des scores moyens très différents (483 pour la France, 515 pour l’Angleterre et les Etats-Unis). En revanche, pour tous les autres déciles et quartiles, la France se situe sous les autres pays avec des différences statistiquement significatives.
La comparaison entre elles des meilleures performances à l’intérieur de chaque pays permet de constater qu’en Quatrième autant qu’en CM1, les meilleures performances françaises sont en moyenne bien en dessous des meilleures performances des autres pays.
On n’observe pas pour l’Angleterre le même phénomène à ce niveau qu’en CM1 : les meilleures performances anglaises ne sont pas meilleures que les meilleures performances russes, japonaises ou singapouriennes. En revanche, on remarque que plus l’on s’approche du haut de la distribution, plus les performances japonaises sont proches des performances singapouriennes.
Du point de vue de l’écart entre meilleures performances et performances de l’ensemble, on constate que la France est, avec Singapour, le pays où il est le plus réduit. Plus précisément, on peut distinguer 3 paires de pays du point de vue de l’écart entre leurs meilleures performances et les performances d’ensemble : France/Singapour, Russie/Japon, Angleterre/USA (où cet écart est très important).
Nous avons également comparé entre elles les moins bonnes performances à l’intérieur de chaque pays et avons pu remarquer que les pays ne s’ordonnent pas du tout de la même façon du point de vue des performances moyennes et des performances moyennes des moins bons élèves. En particulier, les moins bons américains sont significativement moins bons que les moins bons français. Les moins bons anglais sont quant à eux à un niveau statistiquement équivalent à celui des moins bons français. Ainsi, la forte dispersion du niveau constatée en Angleterre et aux Etats-Unis a pour résultat que, malgré des scores moyens bien plus élevés que celui de la France, les moins bons élèves à l’intérieur de ces deux pays réalisent des performances équivalentes, voire moins bonnes, que les moins bons élèves français.
Un second résultat concerne l’écart de performance entre l’ensemble et les moins bons. On note que cet écart est significativement moins important en France que dans tous les autres pays. L’ordre des pays de ce point de vue est le suivant (du plus petit au plus grand écart) : France, Russie, Japon, Angleterre, Etats-Unis, Singapour (ces deux derniers pays étant très proches). Ainsi, si l’Angleterre et a fortiori les Etats-Unis ont des scores fortement dispersés en haut comme en bas de la distribution, Singapour a plutôt des scores très resserrés en haut de la distribution, et un groupe de relativement mauvais élèves qui se détache de l’ensemble. La France se distingue quant à elle par le caractère particulièrement homogène de ses scores estimés, ce qui contraste avec ce que nous avions observé en CM1.
Une analyse sur des données plus complètes permettrait d’évaluer si ce resserrement des performances entre le CM1 et la 4ème correspond à un effet d’âge (ce qui irait dans le sens de l’idée que le système scolaire français parviendrait à résorber au cours de la scolarité les écarts observables en début de primaire), un effet de génération (ce qui pourrait signifier que les élèves nés vers 2010 environ sont plus dispersés du point de vue de leurs performances en maths que ne le sont les élèves nés vers 2006) ou un effet de période (ce qui pourrait vouloir dire que quelque chose s’est passé entre l’entrée dans la scolarité de la cohorte 2006 et l’entrée dans la scolarité de la cohorte 2010 qui explique que les performances en maths de cette dernière soient plus homogènes).
Le graphique suivant permet, comme pour le CM1, de résumer toutes les remarques précédentes :
Densités et boîtes à moustache représentant le score estimé en mathématiques des élèves de Quatrième pour tous les pays en 2019
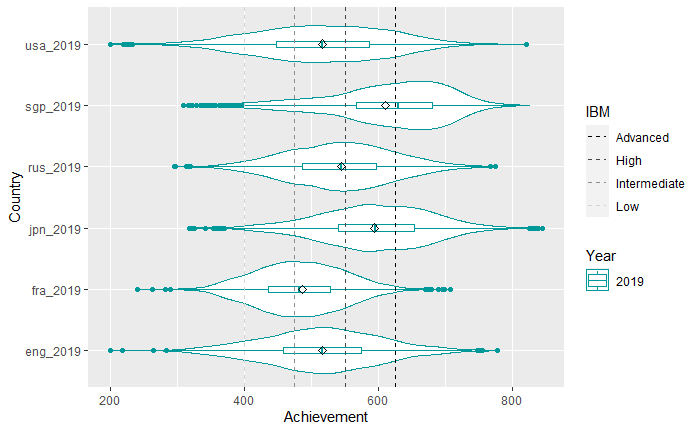
Source : IEA, TIMSS 2019 Database
Enfin, nous nous sommes intéressées à la répartition des élèves dans les différents seuils de niveau fixés par TIMSS, que nous représentons sur le graphique ci-dessous. On note que, contrairement à ce qui avait été observé pour le CM1, la part importante d’élèves très en retard ne s’observe pas uniquement en France mais également en Angleterre et aux Etats-Unis. Nos observations précédentes nous permettent même de comprendre que ces près de 10% d’élèves en retard ont un niveau moyen équivalent en Angleterre et en France, et moindre aux Etats-Unis que dans ces deux pays.
Mais la France se distingue par le fait que cette part élevée d’élèves en difficulté se conjugue avec une part remarquablement faible d’élèves de niveau avancé. En somme, on a observé que les élèves français sont très regroupés, mais ils sont regroupés autour d’un niveau moyen-faible, ce qui explique ces résultats. On notera également que l’Angleterre et les Etats-Unis ont vraiment des profils très proches du point de vue du niveau et de la distribution de leurs performances en mathématiques, avec peut-être de plus fortes disparités de niveau aux Etats-Unis et relativement plus de très bons élèves.
Répartition par seuil de performance en mathématiques des élèves de niveau quatrième pour 6 pays
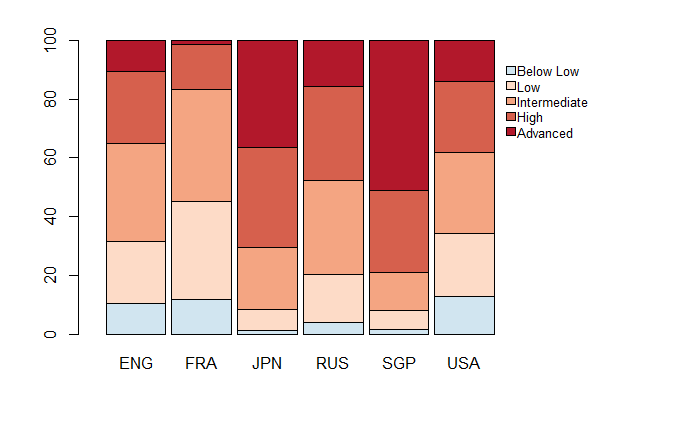
Source : IEA, TIMSS 2019 Database
En conclusion.
En conclusion, on pourra retenir que la caractéristique principale de la France du point de vue de la performance en mathématiques de ses élèves de CM1 et de Quatrième telle qu’elle est estimée par l’IEA est la part importante d’élèves de niveau insuffisant et la part très faible d’élèves de niveau avancé (selon les standards fixés par cette institution).
On retiendra également que les scores français sont moyennement dispersés en CM1, et très peu dispersés en Quatrième relativement aux autres pays étudiés. Ce phénomène est intéressant et gagnerait à être caractérisé et expliqué plus amplement.
On pourra également retenir de cette brève comparaison des scores obtenus par différents pays que l’Angleterre et les Etats-Unis se caractérisent par des très fortes dispersions de leur niveau, surtout en bas de la distribution et surtout en Quatrième. Les pays asiatiques et la Russie semblent au contraire assez homogènes du point de vue des performances en mathématiques de leurs élèves, hormis peut-être dans le cas de Singapour pour lequel on observe un certain décrochage d’élèves de relativement moins bon niveau par rapport à l’ensemble.
De manière générale, ce travail doit nous inciter à la prudence lors du commentaire des résultats des grandes enquêtes d’évaluation du niveau scolaire. En effet, on observe que les commentateurs et commentatrices s’en tiennent souvent à la comparaison de moyennes dans le temps et dans l’espace ; il nous semble avoir montré qu’une exploration et une comparaison des distributions permet de tirer des conclusions plus fines qui peuvent avoir des implications différentes en termes de politiques publiques.
Ces résultats suggèrent en effet pour la France (et dans une moindre mesure pour l’Allemagne) une nécessité de réaliser une translation du niveau aussi bien en haut qu’en bas de la distribution, tandis qu’ils suggèrent plutôt pour les pays anglo-saxons une nécessité de résorber les forts écarts de niveau, et notamment de “rattraper” un groupe d’élèves en difficulté très éloigné de l’ensemble.
On notera au passage que les politiques favorisant l’excellence des meilleurs ne se font pas toujours au détriment des performances des moins bons, puisque des pays comme la Russie et a fortiori le Japon parviennent à combiner une relativement faible dispersion des scores avec des performances classées parmi les meilleures au monde.
Mais, plus largement, il apparaît important de prendre du recul relativement aux résultats issus de ces grandes enquêtes et d’en interroger les fondements épistémologiques, théoriques et parfois idéologiques afin de questionner leur légitimité et leurs effets en tant qu’instruments de l’action publique. C’est ce que nous nous proposons de faire dans un troisième et dernier article (à paraître dans quelques jours), dans lequel nous reviendrons sur quelques résultats issus de la littérature en sciences sociales traitant de l’impact de ces nouveaux dispositifs d’enquête sur le débat et les politiques publiques en matière d’éducation.
Mots-clés : Mathématiques – Enseignement – TIMSS 2019 – comparaison internationale – distribution du niveau
Cet article a été initialement publié le 19 mai 2022.
[1] https://variances.eu/?p=6665
[2] Néanmoins, il faut prendre des précautions au sujet de tout ce qui concerne les groupes des 1% les meilleurs et les moins bons car les effectifs sont vraiment faibles donc les résultats sont moins fiables.
[3] Les traits en pointillé représentent les seuils de niveau (International Benchmarks) fixés par TIMSS, que nous évoquerons juste après.
- Accroissement des disparités genrées de performance en mathématiques en CM1 : une évolution aux conséquences graves - 16 décembre 2024
- Que nous apprend la publication de l’Indice de Position sociale (IPS) des collèges français sur la concentration des élèves d’origine favorisée dans le secteur privé ? - 9 février 2023
- Les Français et les mathématiques : ce que nous apprend l’enquête TIMSS 2019, au-delà des moyennes et des classements - 29 août 2022


Commentaires récents