Coronavirus et comportement individuel [1]

L’épidémie interroge le fondement argumentatif des décisions politiques. Ainsi, quand E. Macron dit « je m’appuie sur les avis des scientifiques », il énonce quelque chose d’inexact : je ne le soupçonne pas de le faire de manière délibérée. Je pense plutôt qu’il souligne ainsi que jusqu’au dernier moment il n’a pas la légitimité politique pour prendre des mesures drastiques. C’est quand nous approchons du mur que lui, comme le plupart des dirigeants occidentaux, peuvent commencer à agir, évidemment avec beaucoup plus de retard que les dirigeants chinois. C’est pour cela que les épidémiologistes comme Q. Lin, N. Fergusson, ou S. Cauchemez en France et leurs collègues développent des simulations mathématiques (vous en trouverez une plus bas si vous souhaitez entrer dans ce labyrinthe), qui sont des descriptions non pas de dynamiques bio-pharmacologiques (Ferguson et al. 2020 le disent expressément), mais de dynamiques bio-socio-politiques.

Il n’appartient pas aux scientifiques en tant que tels de dire ce qu’il faut faire et peu le revendiquent. Or, le Président a institué un conseil dont il dit « suivre les recommandations », il ne se contente pas de consulter les scientifiques. Il y a une incohérence dans cette démarche qui n’est pas seulement formelle. Elle tient au fait que les dynamiques épidémiologiques ne sont pas, à court terme, régies par des variables pharmaceutiques (voir Fergusson et al. 2020). Les comportements sociaux et les actions publiques qui sont déterminantes sont des variables exogènes aux modèles. On ne peut donc attendre de ces modèles qu’une description, plus ou moins précise, des conséquences des dynamiques bio-socio-politiques. Ces dynamiques dépendent à court terme de nos choix et des choix des dirigeants élus. Ils doivent donc prendre leurs responsabilités, ce qui implique précisément de mettre de côté les questions de court terme, élections municipales ou autres.

Auto-protection et/ou coercition

Les pays européens déshabitués des épidémies^[2] ont regardé ce qui se passait en Chine sans agir. Pour ce qui est de la France, du 24 janvier (date du 1^er cas) au 20 mars, les stocks de masques efficaces (FFP2) sont bien gardés, les kits de dépistages ne sont pas disponibles et l’on ne distribue pas en masse des masques chirurgicaux comme l’ont fait les Vietnamiens avec succès. Les autorités nous vantent l’importance des gestes « barrières » dont l’efficacité est douteuse (on indique que les masques sont inutiles, mais que tousser dans son coude est efficace !) En l’absence de remède ou de vaccin, il n’y a pas d’autres moyens d’éviter la propagation du virus que de limiter les contacts infectieux entre des personnes susceptibles (c’est-à-dire quasiment nous tous) et les quelques centaines ou milliers^[3] de personnes infectées au temps t₀, disons le milieu de février en France lorsqu’on a vu que les foyers initiaux de contagion ne pouvaient être circonscrits. La dynamique de l’épidémie, une fois que le virus déborde les petits groupes initiaux qu’on aurait pu isoler, dépend des comportements des citoyens et/ou des restrictions politiquement décidées.

Pour les pouvoirs publics, il est crucial que l’épidémie ne fasse pas trop de malades sérieux car le nombre d’unités de soins intensifs est limité. Pour les gens ordinaires habitués à la grippe, il y a une insouciance large, et sauf quand on est âgé, on ne craint pas d’en mourir. Avec le coronavirus et la publication quotidienne du chiffre des morts, une logique de la peur s’instaure. Les gens ne veulent pas savoir si le taux de létalité est de 2 % ou de 20 % des cas, le seuil psychologique de la peur peut être bas, leur préoccupation est de ne pas entrer dans la catégorie infectés. D’où deux préoccupations différentes : celle des pouvoirs publics qui, idéalement, pensent aux capacités hospitalières, et celle des gens ordinaires qui s’attachent au nombre absolu de cas d’infection et au nombre de victimes.

Qianying Lin (2020) et ses collègues, des chercheurs chinois et américains, dont les attendus épidémiologiques ne sont pas éloignés de ceux de Fergusson, ont réfléchi à partir de ce qui a été observé en Chine, en Corée du Sud, au Vietnam et à Taïwan. Ils ont vérifié qu’en Chine, les actions entreprises reposent sur une restriction forte et précoce des interactions par la combinaison d’une coercition et d’une auto-restriction. La coercition est d’autant moins nécessaire que l’auto-discipline est forte. Ils confirment que la dynamique ne dépend pas principalement de paramètres pharmaceutiques ou viraux, sauf bien sûr la transmissibilité du virus au sens biologique mais d’abord des interactions au sens sociologique : le nombre des contacts qu’a une personne contaminée avec des personnes susceptibles (c’est-à-dire non encore infectées) présentes autour d’elle. Cette quantité de contacts est un paramètre social, qui dépend surtout du mode de vie, de la santé et de l’âge bien sûr, mais aussi politique.

Les autorités chinoises ont confiné autoritairement les habitants de Wuhan et du Hubei chez eux. Ce que Qianying Lin (2020) et al. ont formalisé en un mix chinois fait de coercition et d’auto-limitation. Dans le contexte de l’épidémie de coronavirus, l’action coercitive des pouvoirs publics a réduit drastiquement les contacts^[4]. Ces auteurs ont aussi intégré l’intensité de l’auto-protection, notamment le nombre de personnes avec lesquelles chaque personne infectée interagit en réponse à la pression de la peur indiquée par la proportion des décès dus au coronavirus dans la population. Les restrictions des libertés et des interactions par voie de conséquence, ne font pas qu’aplatir la courbe. Si la seule auto-restriction peut, si l’épidémie dure, n’aboutir qu’à étaler le nombre des contaminations dans le temps, la combinaison avec l’action publique diminue de façon absolue le tribut de contaminations et de morts (si l’on admet que le nombre de décès est proportionnel aux contaminations). Les trois courbes ci-dessous montrent que le nombre cumulé de cas d’infection (la surface sous chacune des trois courbes) est très différent.

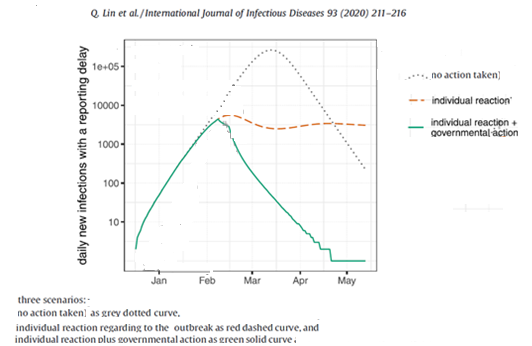
Adapté de Q. Lin & al 2020 par l’auteur.

Selon le modèle de Lin & al., en raison de ces adaptations individuelles conjuguées avec l’action de l’Etat, tutélaire lorsque les citoyens sont très responsables ou coercitive lorsqu’ils le sont peu, le nombre d’infections nouvelles plafonne à un niveau plus bas et plus tôt. Le nombre des nouvelles contaminations n’augmente plus, puis on observe une diminution du nombre de nouvelles contaminations et donc progressivement un arrêt de l’épidémie.

Cette type d’adaptation ne semble pas se manifester en Europe. Je me suis attaché au cas de l’Italie non pas parce que les Italiens, notamment les Lombards auraient été désinvoltes, tout au contraire, mais parce qu’ils préfigurent ce qui se passe ailleurs et parce que je crois (voir Lagrange 2020) que nos attitudes de précaution diffèrent de celles des Chinois, des Vietnamiens ou des Coréens^[5]. Rapidement les Lombards ont cessé d’ignorer les risques et se sont comportés de manière moins désinvolte que beaucoup d’Espagnols et sans doute de Français, dont la défiance par rapport aux consignes publiques reste élevée jusqu’au 17-20 mars. Et pourtant le nombre de contaminations en Italie dépasse aujourd’hui celui de la Chine.

Pour comprendre ces dynamiques divergentes il faut entrer plus avant dans le fonctionnement de l’épidémie. L’idée de base est que l’épidémie fonctionne comme une baignoire. Le compartiment des infectés se remplit quand de nouvelles personnes sont contaminées, et se vide quand les personnes qui étaient dans ce compartiment des infectés guérissent (elles sont supposées immunisées) ou décèdent. Dès lors qu’il n’y pas de masques, on ne peut pas agir sur le taux de transmission biologique, mais on peut réduire l’entrée dans le compartiment infectés par restriction des contacts. En l’absence de dispositions purement coercitives, cette restriction des contacts résulte de ce que les individus font volens nolens : en l’occurrence ils s’abstiennent de sortir et de se rassembler quand ils commencent à voir autour d’eux des personnes sérieusement malades ou apprennent des décès^[6]. D’où l’idée qu’à la place d’un coefficient de transmission biologique du virus, l’exposition des individus s’ajuste à leur pesée de l’épidémie. Au lieu de considérer un coefficient b constant, on retient un coefficient b’= b (1– D/N), où D/N représente le taux de mortalité. Ce coefficient b’ rend compte d’un mécanisme social de régulation de l’exposition. Cette idée a été esquissée dans les analyses rétrospectives des adaptations à la terrible épidémie de grippe espagnole en 1918-19, et a suscité des modèles ajustant l’exposition à la peur.

Le modèle Susceptible-Infectious-Removed classique

Pour engager la réflexion d’un manière concrète et quantifiée sur les ajustements sociaux à la menace du coronavirus, je reprends le modèle Susceptible-Infectious-Removed (SIR), datant de 1927 qui formalise, dans cette version schématique, la dynamique de l’épidémie en considérant une population fermée, sans naissances ni migrations, constituée de trois compartiments : les personnes susceptibles d’être contaminées S, les personnes infectées I, les personnes rétablies (immunisées) ou décédées R (pour removed). $S'{t}$ , $I'{t}$ et $R'{t}$ désignent les variations de ces quantités, mathématiquement les dérivées par rapport au temps. N représente la taille de la population totale.

La dynamique de l’épidémie est exprimée par trois équations ci-dessous, avec un coefficient b constant. Elles traduisent respectivement la variation du nombre de personnes susceptibles (ou « infectables »), de personnes infectées, et de personnes mises hors du circuit de l’épidémie, en fonction du nombre de personnes dans les compartiments S et I :

(1) $S'_{{t}} = -\frac{b}{N} \times S_{{t}} \times I_{{t}} ,$

(2) $I'_{{t}} = \frac{b}{N} \times S_{{t}} \times I_{{t}} - v \times I_{{t}} ,$

(3) $R'_{{t}} = v \times I_{{t}}.$

Comme on le voit :

(4) $S'_{{t}} + I'_{{t}} +R'_{{t}} = 0.$

La population qui compose les trois compartiments S, I et R est constante. Les personnes décédées ou guéries (supposées être vaccinées) sortent du groupe des personnes susceptibles. On peut ici ignorer le rôle de $R'_{{t}}$ l’équation (4) est en quelque sorte comptable.

– b est le coefficient de transition vers l’infection. La progression du nombre des infections dépend directement du nombre de personnes infectées au moment t (I_t), du nombre de personnes susceptibles (S_t), et de ce coefficient de transmission b.

– v définit le rythme de sortie du bassin des personnes susceptibles par guérison ou décès; 1/v est la durée moyenne durant laquelle une personne qui a le virus peut en contaminer d’autres.

Voici un diagramme simplifié dans le plan (S, I) défini par le nombre de personnes susceptibles (l’axe des abscisses) et le nombre de personnes infectées (l’axe des ordonnées). La population susceptible $S_{{t}} = N-I_{{t}}$ , diminue à mesure que les gens guérissent (et sont immunisés) ou meurent.

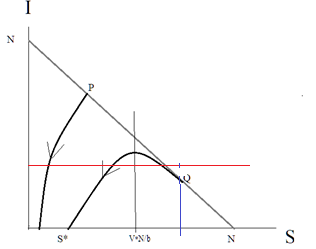
En t=0, on a la relation S₀+ I₀ = N, où N est la population. Tous les points de la droite N-N sont les combinaisons possibles du nombre de personnes initialement susceptibles S₀et infectées I₀. On appelle r₀= bS₀/vN le coefficient de reproduction de base ou d’attaque de l’épidémie, Si r₀>1_,l’épidémie se développe, sinon elle s’éteint (en pratique comme S_͌₀est proche de N, r₀=b/v).

Dans tous les cas le nombre des personnes susceptibles décroît dès le début de l’épidémie, mais deux dynamiques sont possibles. Si l’on part de P, l’épidémie s’éteint de manière monotone. Si l’on part de Q, le nombre d’infections commence par croître, puis atteint un pic au moment où $S=\frac{N}{b}v$ , puis décline vers S*. Une fraction de la population ne sera jamais contaminée. Quand l’épidémie démarre, le compartiment R va se remplir, c’est-à-dire que les individus qui ont été contaminés sont mis hors-jeu, ou plutôt hors risque, étant immunisés ou morts (ce sont les points des trajectoires situés sous la droite N-N reliant l’axe I et l’axe S). Pour les pouvoirs publics, il s’agit que le nombre des contaminations reste au-dessous de la ligne rouge (saturation hospitalière) ; pour les gens ordinaires, il s’agit que les cas cumulés représentés par la surface sous la courbe qui part de Q et bornée par la droite bleue soit la plus petite possible. Je m’attache à la question sociale : la limitation du nombre de cas d’infection. Et une limitation rapide parce que les gens n’entrent pas dans le raisonnement sur l’étalement, ils veulent que la courbe se retourne au plus vite. Ils peuvent accepter les restrictions de leurs mouvements si cette attitude paraît apte à changer les choses. Comment alors évolue I(t), le nombre de cas d’infection[7] ?

En posant S(t) = N – I(t), l’équation (2) peut être écrite :

(5) $I'_{{t}}=\frac{b}{N} \times (N-I_{{t}}) \times I_{{t}} - v \times I_{{t}},$

ou encore :

(6) $I'_{{t}}=\frac{b}{N} \times I_{{t}} \times I_{{t}} + (b-v) \times I_{{t}},$

Si l’épidémie part de Q, elle atteint un maximum quand $S=\frac{b}{N} \times v$ , car dI/dS=0

☐ $d(\frac{b}{N}S-v)I)/ds=0$

Qiang Lin & al. considèrent qu’il y a des adaptations comportementales et que b/N évolue dans le temps en fonction de la peur due aux décès et à l’effet coercitif de l’action publique. J’ai repris l’idée, mais en écartant l’action coercitive et en m’attachant au seul effet des comportements sociaux devant le danger. J’envisage, à la place d’un taux de transmission constant biologique b/N, un taux qui dépend du comportement des individus devant la dynamique épidémique elle-même, avec $b'$ :

(7) $b'=b \times (1-\frac{D(t)}{N}) ^{k}$

Ce coefficient $b'$ d’exposition-contamination dépend de b, le taux de contamination biologique par unité de temps ‘classique’. Il dépend aussi de D(t), N et k :

D(t) désigne le nombre des morts observés dans la région à la date t,

N la taille de la population de la région,

k coefficient d’intensité de la réponse adaptative.

Le facteur d’intensité de l’adaptation k, permet d’exprimer l’idée psychologique que la pression des morts joue à mesure que l’épidémie croît, d’où la puissance k appliquée à une expression entre parenthèses dont la valeur est inférieure à 1. Le spectre des valeurs de k retenues a été établi de manière très empirique à partir des analyses récentes de l’épidémie de 1918^[8].

En formalisant ainsi la dynamique épidémique à l’européenne, j’ai en tête ce qui s’est passé en Lombardie. J’ai fait l’hypothèse que ce ne sont pas seulement les informations circulant dans les médias ou sur les réseaux digitaux qui affectent le comportement de précaution, l’auto-confinement, mais aussi l’émotion ressentie devant la mort de proches. Cela induit des adaptations qui varient avec la sensibilité personnelle et le sentiment de sa propre vulnérabilité. C’est quelque chose que j’ai observé avec la peur du crime : elle est plus fortement dirigée par la fragilité personnelle que par le taux de criminalité objectivable dans la zone de résidence des gens.

Partant de là, j’ai estimé cette dynamique en deux phases. La première phase de 19 jours (j’ai essayé 15 puis prolongé un peu) utilise un coefficient b fixe, car les gens n’ont pas conscience des effets de l’épidémie ou parce qu’il y a de l’inertie dans la prise de conscience. Puis, dans une deuxième phase de 19 jours aussi, j’ai substitué au coefficient b un coefficient b’ qui prend en compte l’émotion suscitée par l’atteinte de proches. Je fais un calcul itératif sur la base d’une discrétisation, comme si les choses changeaient par à-coup d’un jour à l’autre :

(8) S(t) -S(t-1) = – (b/N)S(t-1)I(t-1)

(9) I(t) -I(t-1) = (b/N)S(t-1)I(t-1) -vI(t-1)

Dynamique de l’épidémie en Italie et… en France

Après les premiers jours, la pression du danger est intégrée avec le coefficient b’ définit par l’équation (7), qui remplace b. Les gens s’auto-restreignent mais sans masques ni connaissance systématique des situations d’infection, cela ne permet pas un évitement circonstancié des risques. D’où le fait que l’incurie en matière de dispositifs simples (masques et tests) rend la mobilisation de la population difficile et dangereuse : c’est comme envoyer des soldats au front sans couverture, et cela engendre en conséquence une interruption de la vie sociale.

La population de ma région fictive est 10 millions. On suppose que 90 % des individus sont susceptibles au début de l’épidémie et qu’on observe 470 cas d’infection le 26 février, date de l’irruption de l’épidémie. J’ai pris pour valeur du taux de transmission par unité de temps b = 0,53 (cette valeur correspond à la transmissibilité biologique moyenne au cours d’un contact), v =0,227 est l’inverse de la durée de contagiosité estimée entre 4 et 5 jours (j’ai pris des valeurs en variante autour de 1/5 ou ¼).

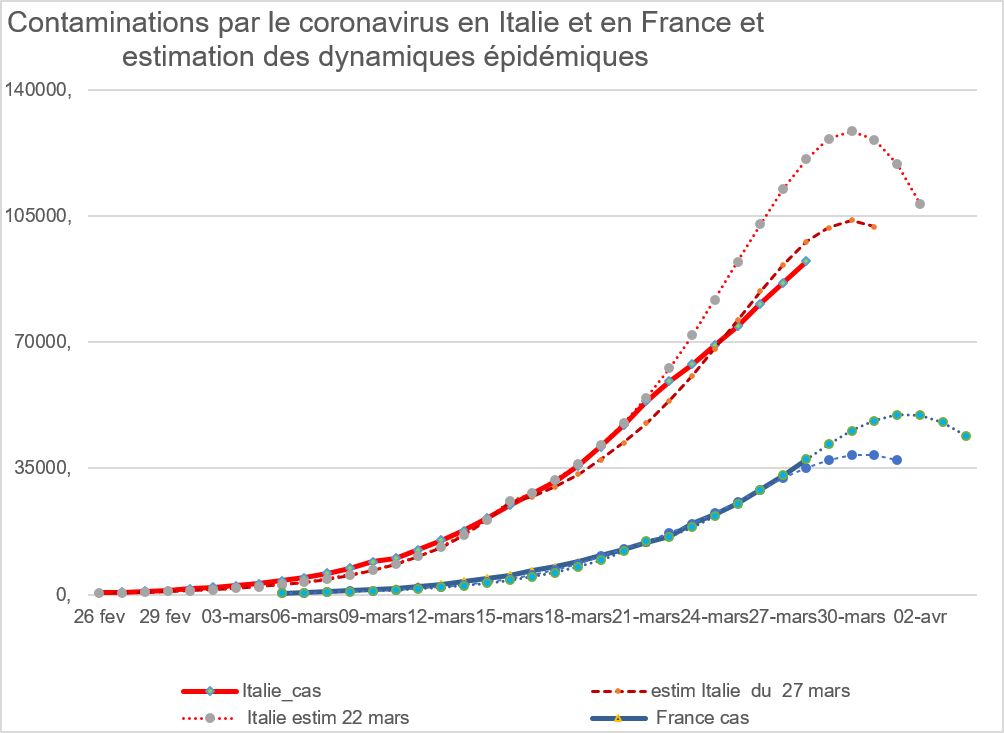
Calculs de l’auteur, code R sur la page OSC Sciences Po de l’auteur.

La France (représentée en bleu) a le 5 mars le nombre de cas de l’Italie (représentée en rouge) le 26 février, soir une retard de 8 jours environ. Le calendrier qui figure en abscisse correspond à l‘Italie. Les données observées, qui ont servi de base à l’ajustement dans les deux pays, suggèrent que l’adaptation à l’épidémie a été plus forte en France. Peut-être parce que les Français voient dans l’Italie ce qui risque de leur arriver ? Peut-être aussi parce que les précautions, encouragées par les pouvoirs publics, ont eu un impact plus précoce, de sorte que l’épidémie monte moins vite en France.

Deux simulations ont été faites le 22 mars et le 28 mars en regard des données italiennes. J’ai supposé que la pesée des décès ne commençait à s’exercer qu’une bonne quinzaine de jours après le 26 février. Les décès en Italie représentent entre 5 % et 15 % des cas d’infection, plus du double de ce qu’ils sont en France, je ne parle pas de l’Allemagne… ni de la Chine hors Hubei.

Cette modélisation s’appuie sur l’idée que les paramètres biologiques^[9] en tant que tels ne disent rien de la dynamique épidémique si l’on ne prend pas en compte les conduites de la population, si l’on ignore la mobilisation citoyenne inspirée par le dévouement et le professionnalisme des soignants en dépit d’une impréparation publique consternante. Evidemment, cette qualité de la réponse médicale peut aussi laisser certains penser que les médecins vont « s’en occuper » et réduire les précautions. Sous cette hypothèse, le modèle montre que la dynamique épidémique change quand la peur s’incarne dans des morts ou des pathologies de proches. Nous ne nous adaptons que tardivement, souvent le nez dans le mur (comme en matière de climat). Ce sont les morts ou les malades dans l’entourage, et la peur qu’ils produisent, qui sont la source d’une émotion forte et induisent un changement des comportements. Certes, cela n’est pas nouveau, mais la crise actuelle pourrait être révélatrice de ce qu’en dépit de la hausse des niveaux d’éducation les comportements restent archaïques, le surmoi est moins actif, semble-t-il, que la peur pour soi et les siens.

Mots-clés : Coronavirus – Sociologie – Modèles SIR – adaptation comportementale – coercition

Neil M. Fergusson et al., “Impact of non-pharmaceutical interventions to reduce COVID-19 mortality and healthcare demand”, Imperial College COVID-19 Response Team, 16 mars 2020.

Qianying Lin et al., “A conceptual model for the coronavirus disease 2019 (COVID-19) outbreak in Wuhan, China with individual reaction and governmental action”, International Joural of Infectious Disease, vol. 93, 1^er avril 2020, p. 211-216.

Hugues Lagrange, Les maladies du bonheur, Paris, Presses universitaires de France, 2020.

Annexe

Pour la présentation formelle, je pars des deux équations concernant la variation du nombre de personnes susceptibles et celles du nombre des infectés.

(a1) $S'_{{t}}=-\frac{b}{N} \times S_{{t}} \times I_{{t}},$

(a2) $I'_{{t}}=\frac{b}{N} \times S_{{t}} \times I_{{t}} -v \times I_{{t}}$

L’équation (2) peut s’écrire :

(a3) I’(t)/I(t) ={ $\frac{b}{N} \times$ (S(t)-v}

d’où : $ln(I_(_t_))= \int \left \{ \frac{b}{N} (S(t) - v \right \}dt +c$ , où c est une constante d’intégration.

Le nombre de personnes infectées à la date t, est donné par l’expression :

(a4) I(t) = C exp( $\int \left \{ \frac{b}{N} (S(t)-v \right \}dt)$ ,

Avec les conditions initiales I(0) = I₀, S(0) = S₀, sachant que b > 0, I₀> 0 et S₀ > 0, on peut encore écrire :

(a5) I(t)= I₀ $\times$ exp( $\int \left \{ \frac{b}{N} (S(t)-1 \right \}dt$ )

Dans cette formulation apparaît le terme r₀= $\frac{b}{N} (S(0)$ , coefficient de reproduction de base ou d’attaque de l’épidémie. Si r₀>1_,l’épidémie se développe, sinon elle n’a pas lieu. Mais la population susceptible S(t) n’est pas fixe car les personnes infectées sont exclues de la population susceptible. Le problème est de savoir comment calculer l’intégrale puisque S(t) dépend de I(t)^[10].

Quand on a une équation de type dP/P(µ- θ P)= dt, on peut envisager une séparation des variables :

1/ P(µ- θ P) = (1/ µ)*[1/P + θ / (µ- θ P)]

Ce qui donne par intégration une fonction logistique :

$\frac{1}{\mu}\left \{ln(P/Po)+ ln \frac{|\mu-\theta Po|}{|\mu-\theta P|\right}$ = t-t_o

Comme $\mu-\theta Po>0$ et $\mu-\theta P>0:$ P(t) = $\mu Po/ \left{ (\theta Po + (\mu -\theta Po) \ast e ^{-[\mu(t-to]}$ , en remplaçant dans cette formule P par I les infectés, µ par (b-v) et θ par b/N :

(a6) $I(t)=\frac{(b-v)Io}{(b/N)Io+(b-v-\frac{b}{N}\ast Io) \times e ^{-[(b-v)(t-to)]}}$ .

Cette formule montre que quand t tend vers l’infini, la proportion (b-v)/b est infectée, ce qui revient à dire avec les paramètres de transmission biologiques du coronavirus 57% : cela n’a évidemment pas lieu parce qu’il y a des comportements adaptatifs.

Certes, tant que le population susceptible n’est pas réduite pas l’entrée d’une fraction significative de la population dans le compartiment contaminé et donc immunisée, la croissance est exponentielle, elle s’amortit à mesure que les confinements sont plus stricts bien avant le freinage logistique.

Q. Lin et al. 2020, s’inspirant de travaux réalisés sur la pandémie de 1918 au Royaume-Uni, retiennent un coefficient de transmission b’ variable dans le temps.

(a7) $b' = b \ast (1-\alpha) \ast (1- \frac{D(t)}{N}) ^{k}$

où

α l’effet de l’action coercitive des pouvoirs publics,
D(t) désigne le nombre des morts observés dans la région à la date t,
N la taille de la population de la région,
k, coefficient d’intensité de la réponse adaptative, proposé dans des analyses récentes de l’épidémie de 1918.

^[1] L’auteur remercie Alain Minczeles et François Meunier pour leurs relectures. Les erreurs lui appartiennent naturellement.

^[2] Voir Lagrange 2020.

^[3] Officiellement 12 cas au 15 février mais, en l’absence de tests un peu systématiques, on ignore le chiffre vraisemblable.

[4] Réduction qui ne serait peut-être pas aussi importante dans certaines fractions de la population, par manque de culture de l’auto-protection, que dans d’autres. En Corée, c’est une modalité peu répressive, informée par un dépistage massif, qui a conduit à une limitation des contacts avec les personnes contaminées. Ce souci d’autrui doit être apprécié.

[5] Même si les gouvernements en Europe après avoir souri des Chinois leur ont emboîté le pas, au lieu de suivre les Coréens et les Vietnamiens.

[6] Nous restons des êtres au cerveau reptilien réagissant, et c’est heureux, à l’émotion devant la maladie et la mort des proches.

[7] Voir Annexe pour la résolution du modèle

[8] On peut utiliser des méthodes de maximum de vraisemblance, mais il faut en intégrer les résultats dans le modèle itératif.

[9] La propagation des contaminations tient aux fait que le virus, projeté dans l’haleine peut atteindre les voies respiratoires d’un interlocuteur et se transmet également par la peau.

[10] Nous explicitons dans un court développement annexe en quoi cette expression, où le nombre d’infections est une fonction continue de t équivaut à celle qui définit la croissance des populations.

À propos
Articles récents

Hugues Lagrange

Né en 1951 à Bourg sur Gironde, Hugues Lagrange après des études d’économie à Paris X, de Sciences politiques à l’IEP de Paris, de mathématiques à Paris VI a soutenu un doctorat de Sciences Politiques à l’IEP de Paris. Entré au CNRS en 1981, il a passé sept ans au CERAT à Grenoble, rattaché depuis 1989 à l’Observatoire Sociologique du Changement à Paris, il s’est intéressé à la socialisation des jeunes dans les quartiers pauvres, au VIH et à l’individualisation des mœurs dont témoignent les pathologies chroniques. Dernier ouvrage paru Les maladies du bonheur, PUF, 2020

Les derniers articles par Hugues Lagrange (tout voir)

A quoi sert la toxicomanie ? Retour sur les drogues addictives - 28 septembre 2023
Infectants & vulnérables : les ambiguïtés du confinement - 7 février 2022
Le Covid19, les gènes et le comportement* - 9 août 2021

Coronavirus et comportement individuel [1]

Auto-protection et/ou coercition

Le modèle Susceptible-Infectious-Removed classique

Dynamique de l’épidémie en Italie et… en France

A propos de l’auteur

Hugues Lagrange

Laisser une réponse Annuler la réponse

A propos de Variances.eu

Abonnez-vous à notre newsletter

Thèmes

Archives

Commentaires récents