La donnée : des tablettes sumériennes aux big data

L’objet de cet article est de présenter les phases principales de l’évolution du concept de donnée depuis l’Antiquité jusqu’à nos jours. Le participe passé féminin substantivé du verbe donner a d’abord eu le sens d’ « aumône, distribution » (1200). Il s’est limité à quelques sens spécialisés en mathématiques (1755) et psychologie. On l’utilise aussi en informatique et statistique, traduit de l’anglais data, pluriel du supin, première forme, du verbe latin dare, « donner » (voir Rey et al., 1993). Dans cette brève présentation de son histoire, nous distinguerons quatre périodes distinctes.

De Sumer au 16^ème siècle

Les données produites pendant cette période concernent essentiellement deux opérations : le dénombrement et l’observation de phénomènes astronomiques.

Le dénombrement a toujours été une opération importante de l’activité humaine. Le recensement des populations en est son expression statistique la plus visible. Les premiers témoignages de mise en œuvre de cette méthode de collecte de données sont gravés sur des tablettes d’argile sumériennes et babyloniennes.

Figure 1: A l’origine

Dès le début de son utilisation (Les paragraphes qui suivent sont basés sur le chapitre 2 de l’ouvrage de Droesbeke et Vermandele (2016).), le recensement s’est avéré être un outil de gestion apprécié des puissants. Si les Mésopotamiens y ont recouru très tôt, on en trouve aussi trace dans l’Egypte ancienne, dès la fin du troisième millénaire avant notre ère. Ces peuples avaient bien saisi l’intérêt de recenser les populations pour savoir combien d’hommes pouvaient participer à la construction des temples, palais, pyramides… ou encore d’utiliser cette technique à des fins fiscales.

Plus une population est nombreuse, plus le recensement s’avère utile. C’est ce qu’avaient compris aussi les empereurs chinois. Quelle que soit l’époque concernée, ceux-ci avaient doté la Chine d’une structure administrative consacrée à ce thème, dirigée par des directeurs des multitudes aux pouvoirs affirmés. Pendant plus de 2000 ans, le recensement a constitué un outil au service de l’administration chinoise.

L’Inde est un autre pays d’Asie qui a procédé dès le 4^ème siècle avant notre ère au dénombrement de sa population. Elle a même été plus loin que cet objectif fondamental en prônant une politique planificatrice d’expansion territoriale et économique basée sur une connaissance approfondie de sa population. Un traité a défini la façon d’y parvenir, l’Arthasastra, rédigé par Kautilya, ministre de l’empire indien des Maurya. Il s’agit d’une méthode dont la minutie est remarquable, tant dans la manière de définir les caractères de la population prise en compte que de la quantité importante de données relevées (voir Hecht, 1987). On imagine sans difficulté que la mise en œuvre de ce type de relevé reposait sur un soutien administratif très dense, encadré par un contrôle policier explicite qui n’incitait pas aux non-réponses.

Cette manière d’agir a mis plus de temps pour être appliquée en Occident. La civilisation grecque accorda moins d’importance à la recherche du nombre d’habitants qu’à celui de la composition idéale de la Cité, chère à Platon, même si Aristote, dans sa Politique, s’attarda à réaliser des travaux de statistique descriptive et comparative. Les Romains reprirent les objectifs originaux : réaliser des recensements périodiques grâce à une structure administrative bien organisée afin de contrôler et d’administrer toutes les composantes de leurs territoires. Initiés sous Servius Tullius au 5^ème siècle avant notre ère et réalisés jusqu’en l’an 73 sous Auguste (année du dernier recensement de l’empire romain), les dénombrements ont fait de la fonction de censeur, comme en Chine, un privilège recherché.

La période du déclin de l’Empire romain et le Haut Moyen Age n’ont pas constitué un terrain fertile pour l’organisation de recensements. Ce n’est qu’entre le 14^ème et le 16^ème siècle, que l’on ressent à nouveau le besoin d’informations, que ce soit au niveau des rôles fiscaux ou à celui des relevés d’ordre religieux (Mentionnons en particulier les ordonnances de Villers-Cotterêts de François Ier, en 1539, et celle de Blois de Henri III en 1579, qui introduisirent respectivement les registres de baptêmes et de mariages).

Dans un autre domaine, l’astronomie, les Babyloniens ont observé les mouvements du soleil et des planètes à intervalles réguliers, obtenant ainsi plusieurs observations d’un même phénomène (voir, par exemple, la tablette d’Ammi-Şaduqa sur Vénus, présentée dans la figure 2, datant du 17^ème siècle avant notre ère et visible au British Museum).

Figure 2: Données vénusiennes

Nous ne connaissons malheureusement pas la manière dont ils ont remplacé ces observations multiples par des « valeurs de compromis ». On possède plus d’informations sur les travaux ultérieurs des astronomes grecs (voir Droesbeke et Saporta, 2010). Ainsi, Ptolémée, astronome du 2^ème siècle, utilisa les relevés antérieurs d’Aristarque de Samos et surtout d’Hipparque et proposa, en présence de plusieurs observations d’un même phénomène, de conserver une seule valeur accompagnée de mesures de variation basées, semble-t-il, sur l’étendue des observations, c’est-à-dire l’écart entre la plus grande et la plus petite d’entre elles. Jusqu’au 16^ème siècle, on préféra retenir une « bonne valeur » — en omettant souvent de justifier l’adjectif utilisé — que recourir à une synthèse systématique. Le premier qui utilisa une moyenne comme « outil de synthèse » est probablement l’astronome Tycho Brahé (1546-1601) dont les nombreuses données sur le mouvement des planètes permirent à Johannes Kepler (1571-1630) d’énoncer les lois qui portent son nom.

En cette fin du 16^ème siècle, on construit des données primaires et individuelles, semblables à celles élaborées dans l’Antiquité depuis l’apparition de l’écriture. Pour ce qui concerne les données résultant d’observations répétées d’un même phénomène, les faibles progrès techniques réalisés dans la recherche d’une plus grande précision des instruments de mesure ont fait croire longtemps qu’une « bonne mesure » était meilleure qu’une agrégation dont on ne soupçonnait pas l’intérêt.

Les 17ème et 18ème siècles

Depuis le 15^ème siècle, de nombreuses villes ont recensé leurs habitants. Les Etats tendant à se centraliser et à se doter d’une administration solide, le besoin de dénombrer se fait à nouveau sentir, même si la pratique est souvent défaillante. Jusqu’à la fin du 17^ème siècle, les registres sont en effet loin d’être parfaits ! Ce 17^ème siècle voit trois courants distincts se développer en Europe : la Staatkunde allemande, les enquêtes de l’administration française et l’arithmétique politique anglaise.

La Staatkunde allemande trouve ses racines dans les travaux d’Aristote. Pour ses défenseurs (parmi lesquels il faut citer le nom d’Achenwall (1719-1772) à qui on attribue la paternité du mot « statistique »), la statistique est la science de l’Etat. Purement descriptive, elle ne fait pratiquement jamais appel à des données chiffrées. Son influence est cependant significative, surtout en Europe centrale, et perdurera jusqu’au 19^ème siècle.

En France, on plaide toujours pour les dénombrements comme outils de gouvernement. Deux hommes se sont particulièrement illustrés dans le recours à des enquêtes en raison des contraintes économiques : Colbert (1619-1683) qui développe une stratégie de dénombrement des villes et des régions, et Vauban (1633-1707), auteur d’une Méthode généralle et facille pour faire le dénombrement des peuples en 1686.

Mais c’est en Angleterre qu’un mouvement novateur se répand avec l’arithmétique politique due principalement à Graunt (1620-1674) et Petty (1623-1687). Comme le dira Charles Davenant (1656-1714), émule de Petty, « l’arithmétique politique est l’art de raisonner par des chiffres sur des objets relatifs au gouvernement ». On y trouve les fondements de la méthode du multiplicateur qui a marqué les techniques de dénombrement des 17^ème et 18^ème siècles, provoquant une mise à l’ombre certaine de la Staatkunde allemande en Europe occidentale.

La méthode du multiplicateur repose sur l’idée suivante : il existe des quantités qui sont en rapports simples et relativement constants avec la population d’un pays. Si ces quantités sont plus simples à dénombrer (nombre de maisons, feux (foyers)… , ou encore nombre de naissances, de décès… dans l’année), il suffit de multiplier leur nombre par un multiplicateur adéquat pour obtenir une estimation du nombre d’individus dans la population. Pour les responsables politiques de l’époque, le recensement d’une population présente des désavantages certains (réactions de méfiance des enquêtés, coûts de mise en œuvre trop élevés…) ; mais d’un autre côté, le choix d’une entité plus simple à dénombrer et la détermination d’un multiplicateur unique posent aussi des problèmes de fiabilité.

Une des caractéristiques du 18^ème siècle – le siècle des Lumières – est le triomphe de l’esprit de calcul. Il faut dire que les progrès réalisés par les mathématiques sont alors considérables et la loi des grands nombres de Bernoulli vient ajouter sa pierre à l’édifice. L’époque est cependant marquée par de nombreuses imprécisions sur les estimations fournies par les uns et les autres. Il n’est donc pas étonnant de constater que les recensements sont revenus en force au 19^ème siècle avant de connaître une stagnation puis un déclin au 20^ème siècle, dû notamment à l’introduction de registres administratifs performants et au développement des techniques de sondage. Mais cela, c’est une autre histoire sur laquelle nous reviendrons ci-dessous.

Parmi les développements qui contribuent significativement à l’évolution de l’histoire des données, il faut souligner l’amélioration des instruments de mesure. Celle-ci est essentielle car elle permet aux hommes de s’aventurer sur les mers en s’assurant une meilleure qualité des moyens de se guider. Par ailleurs, si les mesures astronomiques constituent toujours une manière incontournable — malgré leurs imprécisions — de savoir où l’on se trouve, un autre instrument de connaissance permet de mieux maîtriser le sol sur lequel on vit : la géodésie. Cette discipline et l’astronomie constituent deux domaines privilégiés d’un traitement de données qui se cherche. Un exemple remarquable est celui de la mesure d’un arc de méridien, au centre d’une question primordiale à l’époque : quelle est la figure de la terre ? Le recours à la technique de triangulation est à l’origine d’aventures multiples de cette mesure dans diverses régions du globe qui permettront de résoudre la question (voir Droesbeke et al. , 2016).

Le besoin de mesurer est partagé par de nombreux savants qui bénéficient d’instruments de mesure de plus en plus précis. On devient exigeant à propos de la qualité des observations effectuées et l’erreur de mesure devient un souci essentiel.

Deux approches coexistent pendant de nombreuses années. La première milite pour la recherche d’une bonne mesure, entachée d’une erreur limitée, inférieure à une erreur maximale, acceptable ou en tout cas à craindre. Dans cette optique − défendue par Leonhard Euler (1707- 1783) − prendre en compte d’autres mesures en plus de la bonne ne peut que faire croître l’erreur globale, notamment en utilisant les observations les plus mauvaises.

Un deuxième modèle nous intéresse davantage ici. Il repose sur l’hypothèse que l’utilisation de toutes les observations permet des compensations dont on peut espérer qu’elles réduisent l’erreur résultante. C’est en recherchant des modèles appropriés de distribution des erreurs que de nombreux scientifiques contribueront à la consolidation d’une théorie qui sera qualifiée en 1765 de théorie des erreurs par Johann-Heinrich Lambert (1728-1777).

La multiplicité des observations et le besoin de s’interroger sur le comportement des erreurs de mesure n’amènent pas seulement de nombreux scientifiques à vouloir modéliser cette erreur pour mieux la dompter ; cette question comporte aussi des aspects politiques et commerciaux qui constituent autant d’enjeux importants pour l’époque.

Les données se multiplient et se contredisent. Il faut en comprendre la raison, les gérer pour en tirer profit. Le calcul des probabilités vient en aide à ceux qui affrontent ce problème. Il en résulte une conséquence à trois facettes dont les effets seront durables : la loi des erreurs, qui sera qualifiée de « normale » à la fin du 19^ème siècle, devient une loi de référence, la moyenne s’avère être le mode de synthèse privilégié et un critère d’ajustement devient incontournable : le critère des moindres carrés (voir Droesbeke et Tassi, 2015). Deux hommes jouent un rôle central dans cette histoire : Pierre-Simon de Laplace (1749- 1827) et Carl Friedrich Gauss (1777-1855).

Figure 3: Pierre-Simon de Laplace

Figure 4: Carl-Friedrich Gauss

Les données individuelles deviennent plus fiables ; elles font place aux données agrégées et aux données transformées (voir Droesbeke et Vermandele, 2016).

Quelques points forts du 19^ème siècle

Le 19^ème siècle occupe une place très importante en statistique. S’il fallait retenir cinq caractéristiques essentielles de ce siècle dans l’histoire des données, notre choix serait le suivant :

1. L’application des trois outils utilisés en astronomie (loi normale, critère des moindres carrés et moyenne) à l’étude des populations et de leurs caractéristiques humaines, permettant à Adolphe Quetelet (1796-1872) de créer une théorie des moyennes aux accents multiples (voir Académie Royale de Belgique, 1997, Desrosières, 1993 ou encore Droesbeke et Vermandele, 2016).
2. Le développement de la statistique comme outil de gestion des Etats, au niveau économique et social (voir Desrosières, 1993). Les tables statistiques et les représentations graphiques deviennent un outil important d’analyse et de communication.
3. Le remplacement du rôle central de la moyenne par celui de la dispersion dans les préoccupations des savants de tous bords.
4. Le déplacement du centre de gravité de la statistique vers Londres et l’émergence des concepts de corrélation et de régression (voir Droesbeke et Tassi, 2015 et Droesbeke et Vermandele, 2016).
5. L’émergence d’une nouvelle méthode de recueil des données : les sondages (voir Droesbeke et Tassi, 2015).

Les données individuelles se répandent ; la manière de les produire se diversifie. Elles deviennent nombreuses : il faut les montrer et les résumer.

Le 20e siècle et le début du 21e siècle

Il est difficile de détailler dans cet article les développements de la statistique au 20^ème siècle, tant les innovations sont nombreuses et diversifiées. Il est certain que l’inférence statistique est au centre de ces dernières, avec ses deux problèmes centraux, l’estimation de paramètres d’une population et les tests d’hypothèses réalisés à partir d’un échantillon. La figure 5 nous montre les principaux acteurs et le moment de leur activité la plus intense (en rouge) dans le développement de leurs travaux.

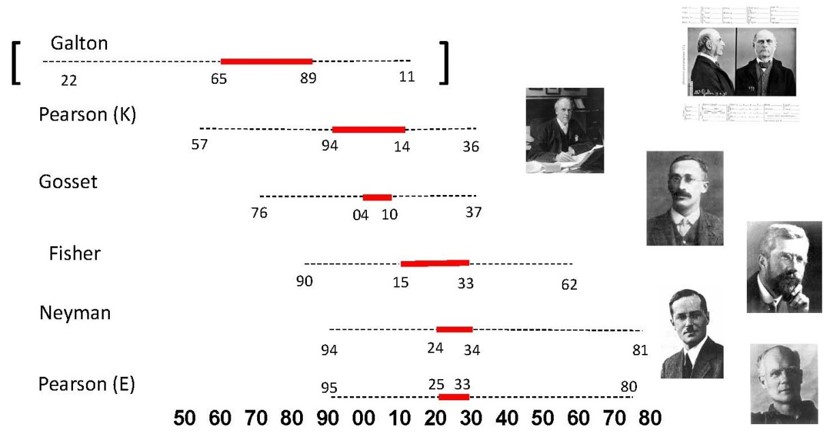
Figure 5: Les moments forts de l’inférence statistique

Nous ne pouvons expliciter ici toutes les ouvertures nouvelles du 20^ème siècle et du début du siècle actuel, qui traitent des données : elles s’appellent plans d’expérience, méthodes de sondage, analyse statistique bayésienne, analyse exploratoire des données, analyse robuste… Parallèlement des stratégies d’analyse ont vu le jour ainsi que des procédures de diffusion des résultats d’analyse appropriées.

Les données sont à présent multivariées, elles sont qualitatives ou quantitatives, il en est de manquantes et d’extrêmes, elles deviennent de plus en plus nombreuses. En ce début de 21^ème siècle, les mégadonnées, encore appelées données massives ou big data nous lancent des défis de toute nature : méthodologiques, techniques, juridiques… Le statisticien de demain se doit de s’ouvrir encore davantage de la science des données.

Bibliographie

• ACADEMIE ROYALE DE BELGIQUE (1997), Actualité et universalité de la pensée scientifique d’Adolphe Quetelet, Actes du Colloque des 24 et 25 octobre 1996, textes rassemblées sous la direction scientifique de J.-J. Droesbeke, Mémoire de la Classe des Sciences, 3^ème série, tome 13.
  
• DESROSIERES A. (1993), La politique des grands nombres. Histoire de la raison statistique, Paris, La Découverte.
  
• DROESBEKE J.-J., MAUMY-BERTRAND M., SAPORTA G. et THOMAS-AGNAN Ch. Eds. (2016), Models choices and agregations, Paris, Technip (à paraître).
• DROESBEKE J.-J. et SAPORTA G. (2010), Les modèles et leur histoire, dans Droesbeke J.-J. et Saporta G. (éds), Analyse statistique des données longitudinales, Paris, Technip, 1-14.
• DROESBEKE J.-J. et TASSI Ph. (2015), Histoire de la statistique, 2^ème édition corrigée, Collection Que sais-je ?, IAD, Paris, Presses Universitaires de France.
• DROESBEKE J.-J. et VERMANDELE C. (2016), Les nombres au quotidien (à paraître).
• HECHT J. (1987), L’idée de dénombrement jusqu’à la révolution, dans Affichar, J. (éd.), Pour une histoire de la statistique, 1, Paris, Economica, 21-81.
• REY A., TOMI M., HORDE T. et TANET Ch. (1993), Dictionnaire historique de la langue française, 2^ème édition, Paris, Dictionnaire Le Robert.

Enregistrer

• À propos
• Articles récents

Jean-Jacques Droesbeke

Professeur émérite de l'Université Libre de Bruxelles

Les derniers articles par Jean-Jacques Droesbeke (tout voir)

• La donnée : des tablettes sumériennes aux big data - 22 juin 2020