CONCEPTS ET REGLEMENTATION AUTOUR DE LA DISCRIMINATION
L’équité actuarielle est un concept clé pour les assureurs, qui signifie que les individus sont traités équitablement en matière de risque. Cela permet leur répartition en classes de risques homogènes, assurant le bon déroulement de la segmentation et de la mutualisation. Mais de nos jours, avec le développement d’algorithmes complexes, des sources de données plus riches et l’amélioration des méthodes d’interprétabilité, de multiples sources de biais ont été exposées et l’objectivité des données et des modèles est remise en question.
Le secteur des assurances fait l’objet d’une attention croissante, le public et les régulateurs exigeant plus de transparence et de justification sur les questions d’équité. Mais il existe une multitude de points de vue sur ce sujet. Premièrement, d’un point de vue juridique, la discrimination est définie par la loi comme la différence de traitement entre des individus se trouvant dans des situations similaires en raison de critères prohibés. Ces critères sont également définis par la loi, mais dépendent de la juridiction. Par exemple, aux États-Unis, selon les États, les informations sur l’origine peuvent être utilisées dans toutes les lignes d’assurance, mais elles sont strictement interdites par la Charte des Droits Fondamentaux de l’Union Européenne.
Lorsque les critères sont utilisés explicitement dans la prise de décision, on parle de discrimination « directe » et lorsque la pratique est apparemment neutre mais conduit tout de même à des traitements différents, on parle de discrimination « indirecte ». Ensuite, d’un point de vue statistique, il existe de nombreuses définitions différentes de l’équité, qui tentent de traduire mathématiquement différentes visions du monde mais ne sont pas compatibles entre elles.
Jusqu’à présent, les actuaires ont empêché la discrimination directe en ne recueillant pas d’informations sensibles [1] sur les individus, conformément au RGPD [2]. Cette méthode n’est pas une solution, car il peut encore y avoir une discrimination indirecte. En effet, si les variables non sensibles ont une relation de dépendance avec les variables sensibles, ce qui est presque toujours le cas, les modèles peuvent déduire ces dernières et maintenir un traitement injuste. Ces variables non sensibles qui permettent d’inférer les variables sensibles sont appelées proxys. De plus, si les informations sensibles ne sont pas collectées, il est impossible de vérifier s’il y a discrimination.
De nombreux articles de recherche ont tenté de fournir une définition mathématique de l’équité. Il existe deux visions : l’équité de groupe, qui vise à traiter différents groupes de manière égale, et l’équité individuelle, qui vise à traiter de manière similaire des individus similaires. Parmi la première catégorie, on peut citer la parité statistique, qui recherche l’indépendance entre la prédiction et les variables sensibles, l’égalité des opportunités, qui recherche l’indépendance entre la prédiction et les variables sensibles, conditionnellement à la vraie classe, qui se traduit par l’égalité des taux de vrais et de faux positifs, et enfin l’égalité des chances qui est la même chose que l’égalité des opportunités, mais uniquement pour les taux de vrais positifs. Aux États-Unis, le Disparate Impact est une mesure populaire qui est une conséquence de la parité statistique et est utilisée dans les tribunaux pour prouver une allégation de discrimination, mais ne s’applique qu’à la classification binaire avec une variable protégée, binaire également. Pour l’équité individuelle, les critères mathématiques ne sont pas aussi simples, car cela implique de définir une distance entre les individus pour mesurer leur similarité, ce qui n’est pas une question triviale.
UNE METHODE DE PRETRAITEMENT POUR ATTENUER LA DISCRIMINATION INDIRECTE
La problématique de ce mémoire d’actuariat est : comment atténuer la discrimination indirecte ? Les solutions consistent généralement soit à travailler directement sur les données (pré-traitement), sur le modèle (pendant le traitement) ou sur les prédictions (post-traitement).
Nous avons décidé de rechercher une méthode de pré-traitement, basée sur l’une des définitions d’équité de groupe, la parité statistique. Cela permet ensuite l’utilisation de tout type de modèle car le problème est traité le plus en amont possible dans le processus, directement sur les données.
Nous nous sommes inspirés du processus de Gram-Schmidt, une méthode d’orthogonalisation d’un ensemble de vecteurs dans un espace avec un produit interne. La covariance est un produit scalaire dans l’espace des variables aléatoires centrées de variance finie. Pour en revenir à la définition de la parité statistique, nous recherchons une prédiction indépendante des variables protégées. Le but de notre méthode est donc de transformer les variables non sensibles de manière à ce qu’elles deviennent décorrélées des variables sensibles. Bien entendu, il s’agit d’une approximation, car la corrélation n’est que la composante linéaire de la dépendance.
La non-corrélation équivaut à l’orthogonalité dans l’espace des variables aléatoires centrées à variance finie, cela nous a donc permis de poser le problème : avec X1, . . ., Xs les s variables sensibles et Xs+1, …, Xn les variables non sensibles, nous cherchons la matrice de passage A qui donne X′ = AX, donnant l’expression des nouvelles coordonnées en fonction des anciennes. Les s premières variables sont inchangées. Cela nous donne une matrice de transition de la forme :
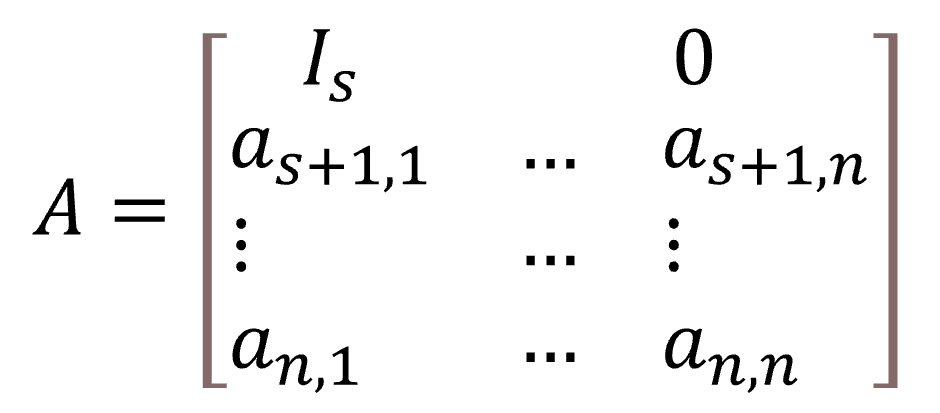
Nous cherchons les variables transformées X′s+1, . . ., X′n telles que corr(Xi,X′j) = 0 pour i = 1, …, s et j = s + 1, …, n. Cela nous donne un système de s équations à n inconnues, avec un nombre infini de solutions car n > s. Nous devons poser n − s contraintes additionnelles de manière à obtenir un système complet. Nous avons fait le choix d’exprimer chaque nouveau vecteur en fonction des vecteurs sensibles ainsi que de son homologue dans l’ancienne base :
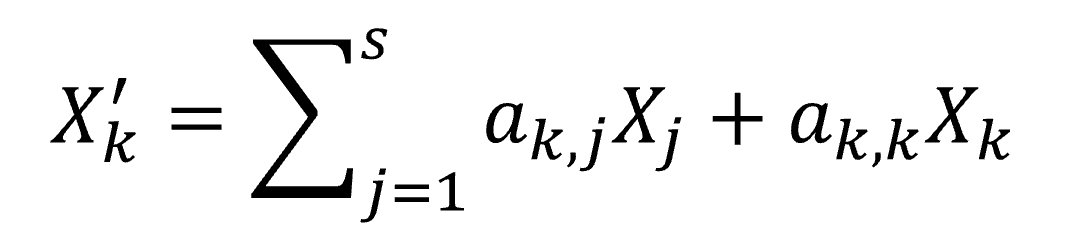
Cela réduit le problème à s équations et s + 1 inconnues. Une idée pour poser la dernière contrainte est de chercher à minimiser la distance entre les anciens et les nouveaux vecteurs non sensibles : min d(Xk,X′k). Le problème a une solution car la distance (correspondant à la variance de la différence des deux variables aléatoires) est positive. Nous avons enfin :
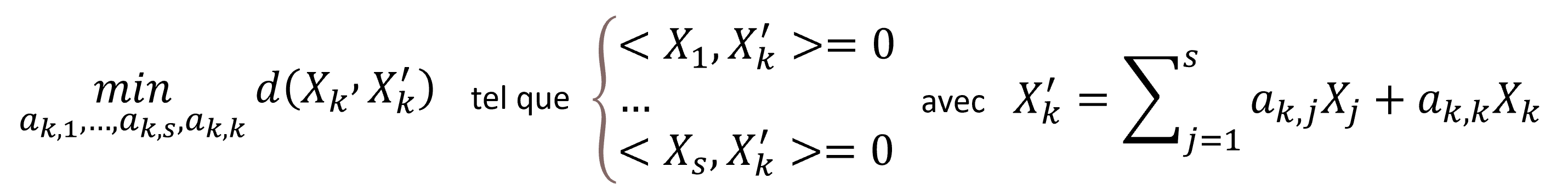
En résolvant le problème pour tous les k = s+1, …, n nous obtenons A et trouvons X′ = AX.
ILLUSTRATION SUR DES DONNEES SIMULEES SIMPLES
Pour illustrer la méthode, nous avons d’abord utilisé des données simulées. La raison est que nous voulons connaître les véritables relations entre les variables, ce qui n’est pas le cas avec des données réelles. Le processus de simulation repose sur la théorie des copules. Nous avons créé un jeu de données avec deux variables sensibles binaires, A et B, quatre variables normales non sensibles, X(1), …, X(4) et une variable d’intérêt binaire. Toutes ces variables sont corrélées entre elles de manière contrôlée. Nous appliquons ensuite un modèle de régression logistique, choisi pour sa simplicité et son interprétabilité, utilisant d’abord toutes les variables, puis uniquement les variables non sensibles et enfin les variables non sensibles transformées.
Le modèle utilisant toutes les variables est, sans surprise, injuste au regard des trois définitions de l’équité introduites précédemment, parité statistique, égalité des chances et égalité des opportunités. Selon les trois définitions, les groupes A = 1 et B = 1 sont désavantagés par le modèle par rapport aux groupes A = 0 et B = 0. Ce modèle fait preuve de discrimination directe car il y a une différence de traitement entre groupes suite à une utilisation explicite des variables sensibles.
Lorsque nous nous contentons de supprimer les variables protégées, il y a une légère baisse de la performance prédictive, mesurée par la précision et l’AUC (Area Under the ROC Curve). En ce qui concerne l’équité, la situation est pire lorsque l’on regarde la variable A, avec le groupe A = 1 encore plus désavantagé par le modèle qu’avant, et meilleure lorsque l’on regarde la variable B, avec le groupe B = 1 toujours le plus défavorisé mais moins qu’avec le modèle utilisant toutes les variables. En n’utilisant pas les variables sensibles, nous avons donc évité la discrimination directe, mais pas la discrimination indirecte car il existe toujours une différence de traitement entre les groupes.
Se contenter de supprimer les variables protégées n’est donc pas une solution pour éviter la discrimination, et selon les relations entre les variables, cela peut soit détériorer, comme nous l’avons vu avec la variable A, ou améliorer l’équité, comme nous l’avons vu avec la variable B.
Enfin, nous appliquons notre méthode de pré-traitement et transformons les variables non sensibles. Les matrices de corrélation avant et après transformation en figure 1 montrent le succès de notre méthode : il n’y a plus de corrélation entre les variables sensibles et les variables transformées.
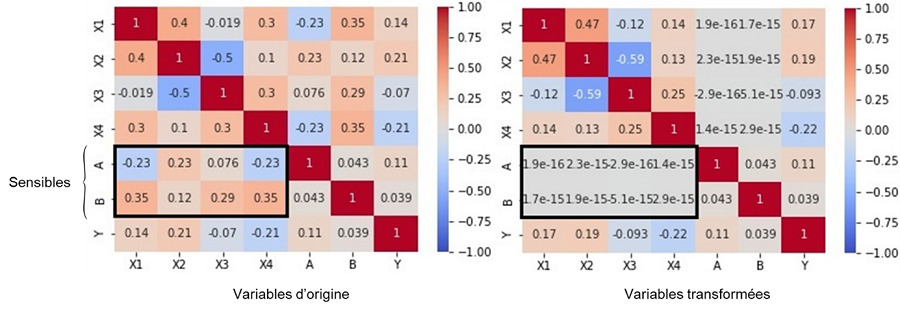
Figure 1 : Heatmaps des corrélations avant et après transformation des X(i)
Nous appliquons ensuite le modèle aux variables non sensibles transformées. Par rapport au modèle utilisant uniquement des variables non sensibles, il y a une baisse de la performance prédictive avec une précision et une AUC inférieures. Le modèle traite désormais presque parfaitement équitablement les groupes selon la définition de la parité statistique, ce qui était l’objectif de la méthode. Mais quand on regarde les deux autres définitions d’équité, pour la variable A, le modèle traite les deux groupes de manière plus juste qu’auparavant, mais maintenant c’est le groupe A = 0 qui est le plus défavorisé. Pour la variable B, le modèle est moins juste qu’avant et encore une fois, c’est maintenant le groupe B = 0 qui est le plus défavorisé selon ces deux définitions.
Notre méthode a approché l’indépendance avec la non-corrélation, et nous avons réussi à approcher la parité statistique. Mais il y a quelques inconvénients : une baisse des performances, des problèmes d’interprétabilité concernant les variables transformées et une incompatibilité avec d’autres définitions d’équité.
ILLUSTRATION SUR DES DONNEES REELLES DE MORTALITE
Nous avons appliqué la même méthode à un cas d’utilisation réel : la mortalité des personnes diagnostiquées avec un mélanome non métastatique, une forme de cancer de la peau. Pour réaliser cette étude, nous avons utilisé les données de la base de recherche publique SEER du National Cancer Institute aux États-Unis. C’est une source d’information très riche et complète, mais qui a nécessité un long traitement avant de pouvoir être utilisée. L’analyse de survie est très spécifique car l’objectif est de modéliser la durée de survie, qui n’est souvent observée que partiellement en raison des phénomènes de censure et de troncature. Pour résoudre ce problème, nous devons prendre en compte l’exposition de chaque individu et l’utiliser comme poids dans le modèle de régression logistique standard.
Une première étape de la modélisation a été la sélection de variables avec trois types de contraintes : médicale, statistique et de souscription. En effet, les variables qui ne sont pas pertinentes médicalement, statistiquement ou qui ne peuvent être obtenues au moment de la souscription ne doivent pas être utilisées dans le modèle. Après cette sélection, il nous reste trois variables sensibles, que sont le sexe (catégories homme, femme), l’origine(catégories White, Hispanic, Black…) et l’état civil (catégories célibataire, marié, veuf…), ainsi que douze variables non sensibles.
Comme pour les données simulées, nous commençons par appliquer notre modèle de régression logistique à toutes les variables. Le modèle fonctionne très bien, avec une AUC de 0,8769. Nous examinons ensuite les mesures d’équité et, sans grande surprise, nous constatons que le modèle n’est équitable selon aucune des trois définitions d’équité. En regardant les taux d’acceptation par origine dans la figure 3a, nous constatons qu’il existe de grands écarts entre les taux d’acceptation, un groupe étant plus défavorisé par le modèle que les autres. Lorsque nous supprimons les variables protégées, il y a, comme dans le cas simulé, une légère baisse des performances, et comme le montre la figure 3b, les niveaux ont changé mais il existe toujours des écarts entre les groupes et le même reste le plus défavorisé. Nous appliquons ensuite notre méthode de décorrélation, et obtenons des vecteurs transformés non corrélés aux vecteurs sensibles. La figure 2 donne la matrice de corrélation avant et après transformation.
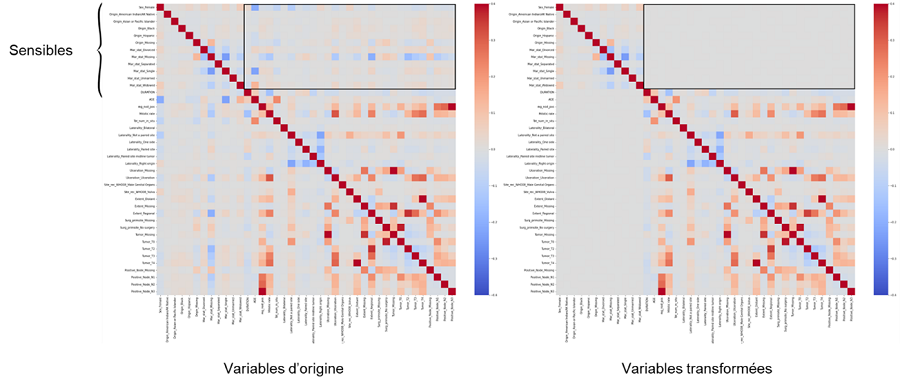
Figure 2 : Corrélations, avant (a) et après (b) transformation, entre les attributs sensibles encadrés en noir et les autres attributs
Lors de l’application du modèle à ces variables transformées, nous avons encore une diminution des performances prédictives avec une AUC plus faible, à 0,8534. En regardant les taux d’acceptation par origine, les écarts sont désormais très faibles entre les groupes. Pour toutes les variables protégées, nous avons la même conclusion : nous avons presque atteint la parité statistique et l’égalité des chances mais nous sommes moins proches de l’égalité des opportunités, et le groupe le plus défavorisé a changé.
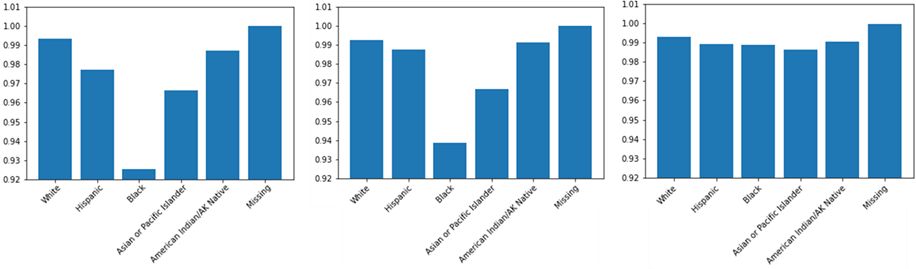
Figure 3 : Taux d’acceptation par origine, avec toutes les variables (a), sans les variables protégées (b) et avec les variables transformées (c), de gauche à droite
EN CONCLUSION
Nous avons les mêmes conclusions que dans le cas simulé : il ne suffit pas de supprimer les variables protégées pour avoir un modèle juste. Notre méthode nous a permis d’approcher la parité statistique, il y a un compromis entre performance et équité, et toutes les définitions d’équité ne sont pas compatibles.
Lien vers le mémoire complet : https://www.institutdesactuaires.com/se-documenter/memoires/memoires-d-actuariat-4651?id=22f397bf2d93510631119af5942bd8da
Mots-clés : équité – discrimination indirecte – parité statistique – décorrélation – Machine Learning – Assurance – Actuariat
[1] Les variables sensibles, aussi appelées protégées, dépendent des régulateurs, mais aussi de la société dans son ensemble, car il s’agit d’une préoccupation à la fois juridique et éthique. Les variables sensibles sont par exemple le sexe, la nationalité, l’état civil…
[2] Le sigle RGPD signifie « Règlement Général sur la Protection des Données ». Le RGPD encadre le traitement des données personnelles sur le territoire de l’Union européenne.


Commentaires récents