Le financement quadratique des biens publics

Cet article a initialement été publié sur le site scienceetonnante.com, le 2 octobre 2023. Il est accessible à l’adresse : https://scienceetonnante.substack.com/p/le-financement-quadratique-des-biens

---

Une formule mathématique bizarre pour mieux financer ces choses qui profitent à tous, mais que personne ne veut payer.

Un article très original traitant de la question du financement des biens publics est sorti en 2019

BUTERIN, Vitalik, HITZIG, Zoë, et WEYL, E. Glen. A flexible design for funding public goods. Management Science, 2019, vol. 65, no 11, p. 5171-5187.

Zoë Hitzig (économiste à Harvard), Glen Weyl (économiste chez Microsoft Research) et Vitalik Buterin (connu pour être le créateur d’Ethereum) proposent de traiter cette question avec un mécanisme utilisant une formule pour le moins étonnante : si chaque individu est prêt à payer une certaine contribution, on ajoute les racines carrées de toutes les contributions et on met le tout au carré.

Ca vous parait absurde, étrange ou incompréhensible ? Voyons ensemble ce que cela cache !

Qu’est-ce qu’un bien public ?

Avant de définir un bien public, commençons par son contraire : le bien privé. Une pomme est un bien privé, car c’est un bien qui est à la fois rival et excluable. « Rival » signifie que si je consomme la pomme, plus personne d’autre ne peut la consommer. « Excluable » veut dire que si j’ai une pomme, je peux facilement empêcher les autres de la consommer. La quasi-totalité des biens que nous croisons tous les jours (objets, marchandises et autres denrées) sont des biens privés.

Au contraire de ça, un bien public est un bien non-rival et non-excluable. « Non-rival » veut dire que si j’en profite, ça n’empêche pas les autres d’en profiter aussi. « Non-excluable » signifie qu’il est difficile voire impossible d’empêcher quiconque d’en profiter, même ceux qui n’ont pas participé à son financement. Des exemples de biens publics, ce sont : l’éclairage public, un parc municipal, des infrastructures de transport (routes ou transports publics gratuits), la radio, la connaissance scientifique, Wikipédia, la défense nationale, des vidéos Youtube, le journalisme d’investigation, un artiste de rue, un logiciel open-source…

Evidemment, dans mes exemples il y a des nuances. Certains biens peuvent être légèrement rivaux (une route ou un parc municipal) car il peut y avoir congestion. D’autres peuvent être excluables à un certain degré (les transports, les contenus sur Internet…). On trouve parfois une classification plus fine suivant les degrés de rivalité ou d’excluabilité, mais dans la suite j’utiliserai de façon générique le terme « bien public » pour désigner ces biens qui répondent en gros à l’idée suivante : « une fois que c’est là, ça profite à tout le monde, indépendamment de qui l’a financé ».

Et donc justement, puisque les biens publics profitent à tous, ou du moins à ceux qui ont l’envie d’en profiter, comment les financer de la meilleure façon possible ?

Deux solutions imparfaites

Une première possibilité, c’est de se reposer sur des contributions volontaires et charitables. C’est ce qu’il se passe quand un artiste chante dans la rue et que certains lui font un don. Ou bien encore avec Wikipédia, financée par les dons de (seulement) quelques millions de ses utilisateurs. Ou encore pour un journal comme le Canard Enchainé, financé par ses lecteurs mais dont tous le monde profite des enquêtes d’investigation.

Sur ces exemples, on voit très bien le problème de se reposer uniquement sur les contributions volontaires et charitables pour financer les biens publics : personne n’a d’intérêt fort à donner, et une partie des utilisateurs se comportent en passagers clandestins : ils profitent du bien public sans le financer. Cette absence d’incitation conduit presque toujours à un sous-financement du bien public par rapport à ce qui serait optimal pour l’ensemble du groupe.

Une solution alternative pour financer un bien public, c’est qu’un organisme centralisé (état, municipalité…) s’en charge, en ayant préalablement collecté les fonds nécessaires. C’est ce qu’il se passe bien sûr avec la plupart des services publics essentiels. Et pourtant, cela pose la question de comment choisir les biens publics à financer. La moins mauvaise solution semble de s’en remettre à un choix démocratique, où l’organisme central prend ses décisions sur la bases des votes de sa population.

Mais cela n’est pas si simple ! Imaginons une petite ville qui envisage de réhabiliter une friche pour en faire un parc municipal. Supposons qu’un tel parc soit une véritable amélioration pour 40% de la population, qui en bénéficierait grandement. Mais imaginons que les 60% restants s’en fichent, peut-être parce qu’ils ont déjà un jardin, et ne voient pas pourquoi la ville ferait cette dépense. Un vote démocratique sur la question « Faut-il créer le parc municipal ? » recueillerait donc une majorité de «non». Le projet ne se ferait pas alors que 40% en tireraient un très grand bénéfice, tandis que les 60% restants sont juste faiblement contre. C’est une forme de ce qu’on appelle parfois la tyrannie de la majorité, qui ici refuse la création d’un bien public au détriment d’une minorité qui en aurait grandement profité.

On peut également prendre des exemples plus modernes : une fondation souhaite financer des développements de logiciels open-source, comment choisir lesquels ? Comment faire si un projet n’intéresse qu’une minorité d’utilisateurs potentiels, mais que cela leur apporterait un bénéfice énorme ?

Bien souvent dans ces cas, on retombe de fait dans le financement volontaire charitable (avec son problème de passager clandestin), et même pour beaucoup de projets, le financement n’aboutit simplement pas !

On voit par ces exemples que le financement efficace des biens publics pose question. Il existe une solution intermédiaire, qui mélange une source de financement centrale avec des contributions volontaires permettant aux agents d’exprimer leurs choix : l’abondement.

L’abondement

C’est un mécanisme que l’on retrouve assez fréquemment dans les politiques publiques : un organisme central choisit de ne pas décider parmi les biens publics à financer, mais s’engage à abonder les contributions volontaires de ses agents. On le voit parfois avec certaines actions philanthropiques, qui proposent par exemple de doubler les contributions des dons privés (un article sur le sujet)

Mais on le retrouve aussi pour les gouvernements, avec le mécanisme du crédit d’impôt ou de la défiscalisation. Par exemple, si vous payez des impôts en France, certaines de vos contributions charitables à des organismes d’intérêt public peuvent donner lieu à des réductions d’impôts. Vous donnez 100€ aux Restos du Coeur, l’état vous donne un crédit d’impôt de 75%, votre don ne vous aura coûté que 25€. Ou bien autre façon de le dire, vous donnez 25€ et l’état abonde le triple de cette somme (avec un plafond à 1000€ en France, ensuite c’est 66%).

Ce principe d’abondement permet dans une certaine mesure de corriger certains défauts de la contribution charitable pure, et de la décision centralisée pure. Néanmoins, on voit aussi ses limites. D’une part les montants et les seuils utilisés sont souvent arbitraires. D’autre part le calcul est critiquable, car l’abondement pour une personne qui donne 500€ sera identique à celui de 50 personnes donnant 10€. Ce qui semble en tension avec l’idée démocratique que si 50 personnes veulent une chose, l’état devrait y accorder plus de poids que si c’est une seule personne.

Et c’est en partie pour répondre à cette tension que Vitalik Buterin, Zoe Hitzig et Glen Weyl ont proposé en 2019 un nouveau mécanisme : le financement quadratique. L’idée est simple, bien qu’un peu bizarre au premier abord.

Le financement quadratique

Avec le financement quadratique, si des agents souhaitent financer un certain bien public, ils peuvent faire une contribution de leur choix. L’organisme central collecte ces contributions volontaires et finance alors le bien public avec le montant suivant : on prend la racine carrée de chaque contribution, on les ajoute, et on met le tout au carré. Hein, quoi ? Prenons un exemple !

Imaginons qu’il n’y ait que deux personnes intéressées. Alice décide de contribuer d’une somme a, et Bob de contribuer d’une somme b. L’état collecte les contributions a et b, et affecte au financement du bien public la somme suivante :

On a pris les racines des deux contributions, on les a ajoutées, et on a mis la somme totale au carré. Ca ne semble pas avoir beaucoup de sens de prendre la racine carrée d’une somme d’argent, mais développons le carré pour voir (souvenez vous de vos identités remarquables)

On voit que le niveau de financement total F est égal à la somme des contributions initiales (a+b) augmentée d’un abondement égal à

C’est un terme qui « croise » les contributions d’Alice et de Bob.

Et on peut appliquer cette logique quand il y a un nombre quelconque d’agents. Le niveau de financement sera toujours égal à la somme des contributions d’origine, augmentée d’un abondement qui correspond à tous les termes croisés possibles entre tous les agents. Pour les fans de formules

En particulier, on voit que si N personnes sont intéressées et mettent toutes la même contribution X, le niveau de financement total sera

et augmente donc avec le carré du nombre de personnes impliquées ! Si on revient à l’exemple du financement d’un parc municipal ou d’un logiciel, 100 personnes qui contribuent chacune 10€ engendreront un abondement 10 fois plus important que 10 personnes qui contribuent chacune 100€.

Quand le nombre de participants devient important, on arrive donc vite à des cas où la majorité du financement provient de l’abondement, en accord avec une logique de planification centralisée, mais où les petites contributions volontaires permettent d’orienter les choix publics.

Evidemment, cela suppose qu’il y a un pool d’argent central à affecter, et donc que cet argent a été collecté d’une façon ou d’une autre (impôt dans le cas d’une puissance publique, philanthropie dans le cas d’une fondation, etc.). Si la formule quadratique aboutit à un abondement qui dépasse le montent de l’argent central disponible, il est toujours possible de réaliser un prorata.

Alors il est vrai que ce mécanisme a l’air plutôt sympathique, mais pourquoi cette formule quadratique bizarre ? Eh bien parce que c’est la meilleure possible ! Au moins…en théorie ! On a vu que le fait de prendre le carré de la somme des racines fait apparaitre des termes croisés pour toutes les paires d’agents. Ces termes représentent intuitivement le caractère « public » du bien : le niveau d’investissement d’un agent aurait des conséquences positives sur tous les autres agents, mais comme ce bénéfice croisé n’est pas pris en compte dans les choix individuels, les agents sous-financent, et c’est donc l’état qui abonde cette contribution croisée.

Mais on peut formaliser ça avec des maths ! C’est très joli, les allergiques peuvent sauter la partie à venir.

L’optimalité du financement quadratique

Dans cette partie, je vais exposer la démonstration de Buterin, Hitzig et Weyl qui démontre que le financement quadratique est le meilleur mécanisme possible, celui qui aboutit au niveau de financement optimal d’un bien public. Tout cela est évidemment très formel, et repose sur les hypothèses habituelles de ces raisonnements micro-économiques mathématisés (tout le monde est rationnel, a toutes les informations, agit de façon purement égoïste, etc.)

Pour introduire les idées, commençons par le cas simple d’un unique agent qui cherche à déterminer son niveau de contribution pour l’achat d’un bien privé, par exemple des pommes. Disons que le kilo de pommes coûte 3 euros, combien doit-il en acheter ? Eh bien cela dépend évidemment de son envie de pommes ! Pour cela, les économistes utilisent une quantité qu’ils appellent l’utilité. Attention, ce terme d’ «utilité» a un sens différent du sens commun usuel. Il désigne en quelque sorte le niveau de bonheur, de satisfaction ou encore de bien-être des agents, que leur procure une certaine quantité d’un bien. L’utilité, c’est ce qu’un agent cherche à maximiser quand il prend une décision.

Si mon agent a faim et apprécie les pommes, acheter des pommes engendrera un certain niveau d’utilité pour lui. Mais cette utilité va évidemment dépendre de la quantité achetée. S’il achète un kilo (pour 3€), il aura un certain niveau de satisfaction. Mais s’il achète 2 kilos (pour 6€), il aura une satisfaction plus élevée. Pour autant, avec 2 kilos, sa satisfaction ne sera probablement pas le double d’avec 1 kg. Chaque pomme supplémentaire qu’il acquiert continue d’augmenter sa satisfaction, mais moins que la pomme précédente.

Cela signifie qu’on a une relation de ce genre :

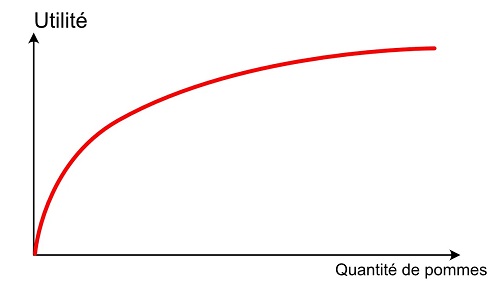
Mathématiquement, on dit que la fonction d’utilité est concave. Une autre façon de le dire, c’est que sa dérivée est décroissante, la pente de la courbe est de plus en plus faible, ce qui traduit le fait que chaque unité supplémentaire apporte moins de satisfaction que la précédente : on parle d’utilité marginale décroissante.

Dans le cas précédent, j’ai illustré l’utilité comme étant une fonction de la quantité. Mais si on se place dans un cas où le coût unitaire est connu et fixe, on peut simplement prendre l’utilité comme une fonction de l’argent dépensé. Ainsi u(x) représentera l’utilité associée à l’achat d’un montant x de pommes.

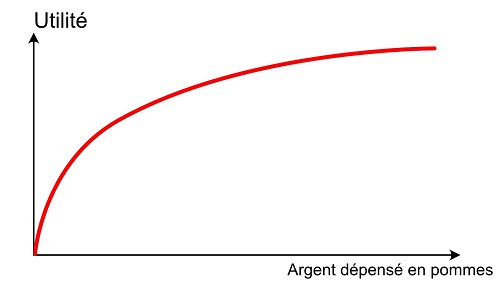
Mais au fait, avec quelle unité on compte l’utilité ? Eh bien on peut parfaitement la compter en unité monétaire également. Si l’achat d’un bien procure une utilité de 10€, cela représente une satisfaction qui est équivalente à celle de posséder 10€ en argent. Oui je sais, c’est bizarre de compter le bonheur en euros, mais c’est une modélisation mathématique simplifiée !

Imaginons donc que l’on connaisse u(x), l’utilité (en euros) associée à l’acquisition de pommes pour un montant total x. Combien faut-il en acheter ? Faisons le bilan net de l’opération : si on dépense x pour acquérir des pommes, notre utilité augmentera de u(x) du fait de la possession des pommes, mais en contrepartie diminuera de x du fait de l’argent dépensé.

L’utilité nette n(x) est

Cette utilité nette va avoir une forme de ce type

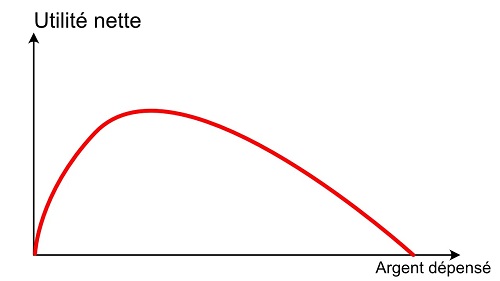
On voit qu’elle possède un maximum. Maintenant ce que cherche à faire un bon agent économique rationnel, c’est à maximiser son utilité nette. Il doit donc trouver la quantité x* qui correspond à ce maximum.

Un maximum est en particulier un point où la dérivée de n() s’annule. On veut donc trouver x* tel que n’(x*) = 0. Puisque n(x)=u(x)-x, on veut trouver x* tel que

Retenez bien cette égalité, elle est fondamentale. Elle montre que le choix optimal, c’est de dépenser la quantité x* pour laquelle la dérivée de l’utilité associée au bien est 1. La dérivée de l’utilité, on l’a dit, c’est l’utilité marginale, c’est-à-dire l’utilité supplémentaire associée à une dépense supplémentaire de 1. Si cette dérivée vaut 1 en x*, ça veut dire qu’on a atteint le point d’indifférence : 1€ en argent ou 1€ de pommes supplémentaires, ça nous procure le même plaisir.

Ca, c’était pour un bien privé financé par un unique agent. Passons maintenant au cas d’un bien public !

Imaginons qu’il y ait N agents (indicés par i), et que chaque agent puisse faire une contribution x au bien public. Dans le cas de contributions charitables et volontaires, le niveau de financement total F du bien public sera simplement la somme des contributions

Imaginons que chaque agent ait une utilité u() qui lui soit propre, et qui soit une fonction non pas de sa seule contribution, mais du montant total auquel a été financé le bien commun. (C’est intuitif : plus le parc a reçu un financement total important, plus il procurera de plaisir aux agents) Chaque agent a donc une utilité qui dépend de F

Son utilité nette sera donc

Si chacun optimise égoïstement, cela veut dire qu’il cherche son niveau de contribution qui maximise sa propre utilité nette. En annulant la dérivée de l’utilité nette par rapport à à sa contribution x_i, on trouve :

où on a utilisé de façon cruciale que

puisque F est une simple somme des contributions.

Maintenant regardons l’utilité nette totale de l’ensemble du groupe, si un niveau global de financement F pour le bien public a été atteint. Elle vaut

Si le choix global était socialement optimal, la dérivée par rapport à F de cette quantité devrait être nulle. Cela signifierai que collectivement, avoir dépensé 1€ de plus n’aurait pas amené plus d’utilité globale. Regardons si c’est le cas ! On dérive cette utilité nette par rapport à F

Utilisons maintenant ce qu’on a vu au dessus, c’est-à-dire que chaque agent a réglé sa propre contribution de façon à ce que

Cela signifie que dans la somme sur i dans l’expression de N’(F), chacun des termes de la somme vaut 1. On a donc pour la dérivée de l’utilité totale nette

Elle ne vaut pas zéro (sauf si N=1), et donc on est pas à l’optimum. Plus précisément, le fait que cette dérivée, qui est l’utilité marginale collective, soit positive (et même très positive si N est grand) cela signifie que l’on pourrait encore largement augmenter l’utilité totale si on arrivait à augmenter le niveau de financement. Le bien public est donc largement sous-financé. Si chacun optimise égoïstement dans son coin, on est loin de l’optimum social.

Voyons maintenant le mécanisme de financement quadratique. Il est en fait très similaire à ce qu’on vient de faire, à part qu’on a maintenant comme fonction de financement

Si on reprend le raisonnement tenu par chaque agent, qui cherche à trouver la contribution qui maximise sa propre utilité nette, on trouve maintenant quelque chose de plus compliqué. En dérivant par rapport à x_i on trouve

Et donc l’annulation de la dérivée donne

On peut calculer explicitement la dérivée partielle pour le mécanisme F de financement quadratique, on trouve alors que

On peut revenir à notre calcul de la dérivée de l’utilité nette globale, et injecter cette valeur dans

Et je vous laisse vérifier qu’on trouve que c’est zéro ! (là où on trouvait N-1 avant). On est à l’optimum social. Le financement quadratique permet donc de faire en sorte que l’on atteigne le niveau de financement optimal, même si chaque agent optimise son utilité dans son coin.

Que faire de ce mécanisme ?

Je vous l’accorde, tout cela est très théorique, mais ça me semble suffisamment intéressant pour qu’on se penche un peu dessus. Il y a plein de problèmes d’implémentation déjà relevés par les auteurs dans leur papier (voir également cette critique), comme par exemple la nécessité d’assurer une identité unique pour chaque agent (qu’il ne puisse pas contribuer sous deux noms différents) ou encore d’éviter les collusions (“je finance ton truc pour que tu finances le mien en retour”).

Néanmoins, l’idée me semble suffisamment stimulante pour que l’on puisse imaginer des tests à petite échelle (attribution de financement participatif par exemple), et voir ce qu’il en retourne ! On pourrait aussi imaginer des variantes intermédiaires entre le financement participatif volontaire et le financement quadratique, avec une formule du type

En particulier on voit que dans la vraie vie, le financement participatif volontaire donne des résultats moins pires que la théorie (qui prévoit essentiellement que personne ne fait quoi que ce soit). Les gens sont moins égoïste que ce que ne prévoit la théorie de l’homo economicus ultra-rationnel (ou plutôt, ils comptent dans leur utilité le plaisir de contribuer à une bonne cause…) Donc peut-être qu’un mécanisme de financement moins ambitieux que le financement quadratique (alpha=1.5 par exemple) donnerait déjà des résultats intéressants sans avoir un effet d’explosion de l’abondement dès qu’on est beaucoup.

Si le sujet vous intéresse, vous pourrez aussi avoir envie de lire des choses sur le vote quadratique, un mécanisme relié, ou encore les radical markets, qui proposent en plus un mécanisme original de taxe pour financer l’abondement. J’en parlerai un jour !

 

Mots-clés : Financement – Biens publics – Abondement – Fiscalité – Utilité

 

Cet article a été initialement publié le 5 octobre 2023.