Après un Mastère Spécialisé en Data Science à l’ENSAE, Caroline Boudier a effectué son stage de fin d’études à la Direction des Applications Militaires du CEA. Dans cet article, elle résume ces quelques mois d’exploration autour de l’application d’un modèle innovant de Deep Learning (les Réseaux de Neurones Inversibles) à la simulation des systèmes physiques régis par des lois énergétiques.
Introduction : principe et enjeux de la simulation
En physique, la simulation numérique est un outil important qui permet d’analyser, de comprendre et de prédire le comportement et l’évolution de systèmes à différentes échelles. Depuis le traité d’interdiction complète des essais nucléaires (1996), elle est également devenue un pilier crucial de la stratégie de dissuasion française.
Si l’approche existe depuis bien longtemps, ses principaux défis n’ont pas changé : précision de la modélisation et réduction du temps de calcul.
Dans le champ de la physique, les méthodes classiques – dites itératives – sont largement utilisées afin de modéliser l’évolution dynamique de systèmes. Mais elles montrent bien souvent leurs limites : un besoin important en ressources de calcul qui peut devenir prohibitif.
Face à ce défi, l’Intelligence Artificielle est une piste intéressante pour mettre en place des modèles moins gourmands en ressources. Mais comment faire en sorte que le gain en efficacité ne s’accompagne pas d’une opacité accrue de modèles « boîtes noires” peu interprétables et explicables ?
Dans le cas des systèmes régis par des lois énergétiques, les Réseaux de Neurones Inversibles pourraient bien apporter une première solution, comme le décrit cet article.
La simulation appliquée aux systèmes régis par des lois énergétiques
Les applications de la simulation en physique sont nombreuses. On y a recours lorsque les simples équations physiques ne permettent pas de totalement appréhender un phénomène du fait de sa complexité. À partir d’hypothèses, on lance alors une simulation : un modèle dit “génératif” produit des échantillons qui correspondent à des configurations du système. À partir de ces configurations il est possible de dériver des propriétés clés du système.
Pour prendre un exemple plus parlant, Noé et al [2] s’intéressent aux protéines : des structures complexes qui peuvent adopter une grande variété de configurations différentes. Chacune de ces configurations est associée à une probabilité d’apparition. L’objectif de la simulation est de générer des échantillons représentatifs de cette distribution. Or les protéines ont tendance à rester infiniment longtemps dans certaines configurations plus stables que d’autres (configurations « pliées » ou « dépliées« ). La distribution est déséquilibrée et les événements de transition (dépliement ou repliement) sont très rarement observés : on les appelle « événements rares ». Ils représentent un défi pour les méthodes statistiques classiques.
Plus généralement de nombreux systèmes physiques suivent ce genre de distributions déséquilibrées, régies par des lois énergétiques. La distribution sous-jacente (dite de Boltzmann) traduit le fait que les systèmes se stabilisent autour d’états dont l’énergie est minimale : la probabilité d’un état est d’autant plus forte que l’énergie associée à cet état est faible. Les états les plus stables sont les plus fréquents et la transition entre deux états stables est très difficile à observer. Pourtant cette transition intéresse beaucoup les scientifiques car c’est elle qui révèle les quantités thermodynamiques d’intérêt du système.
L’étude d’un cas d’école en physique (le potentiel de Mueller) permet de simplifier le problème tout en retrouvant les contraintes des systèmes physiques réels. Il s’agit d’un problème en deux dimensions dans lequel on cherche à échantillonner la position d’un point (défini par ses coordonnées x1 et x2) dans un paysage énergétique composé de deux puits principaux d’énergie comme le montre la figure ci-dessous.
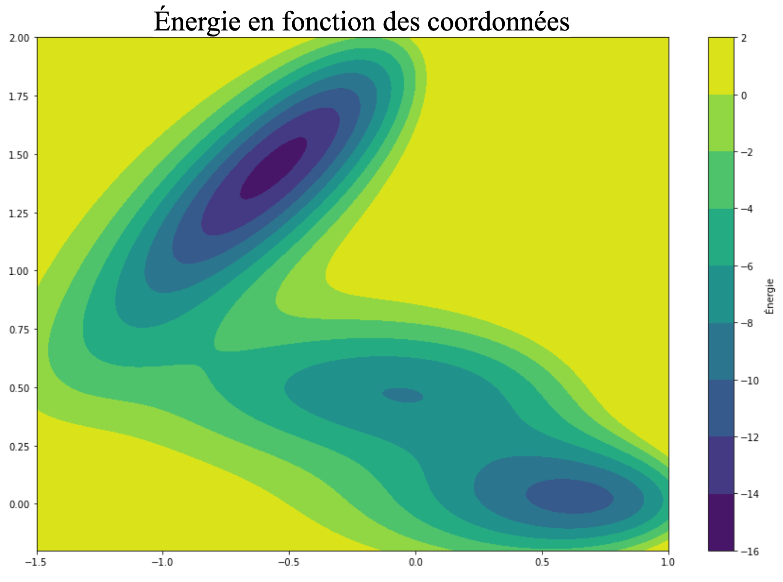
Variation en énergie sur le potentiel de Mueller
L’idée de la simulation est d’obtenir un échantillonnage cohérent avec l’énergie (les zones d’énergie les plus faibles – plus foncées sur le graphe – doivent être sur-représentées) et diversifié (un maximum de configurations doivent être représentées et on veut notamment observer le chemin de passage d’un puits à l’autre).
L’approche traditionnelle : les méthodes itératives
À ce jour les méthodes les plus classiques pour aborder ce type de problèmes en physique sont des méthodes itératives (de type MCMC : Monte Carlo par Chaîne de Markov, ou Dynamique Moléculaire). L’idée est de partir d’une configuration initiale puis de lui appliquer successivement de légères modifications pour observer son « déplacement ». Les modifications apportées sont liées à des éléments de théorie physique qui assurent la pertinence de l’échantillonnage.
Ces approches présentent deux problèmes majeurs. Tout d’abord, elles requièrent de partir d’une configuration donnée puis d’attendre que le modèle ait produit suffisamment d’échantillons pour qu’on puisse considérer les points échantillonnés comme indépendants. Cela représente (surtout en grande dimension) un coût énorme en calcul.
Deuxièmement, ces méthodes sont très dépendantes de leur initialisation. Dans le cas des distributions étudiées (fondées sur l’énergie) les méthodes restent piégées dans des configurations d’énergie faible sans pouvoir passer les barrières énergétiques permettant de visiter d’autres états. Dans le cas d’une protéine, si on lance une simulation classique à partir d’une configuration pliée, le temps nécessaire pour observer le « dépliement » sera extrêmement long, voire infini.
Dans l’exemple du potentiel de Mueller, les simulations itératives (MCMC) restent piégées dans le puits d’énergie le plus proche du point de départ comme le montre la figure ci-dessous.
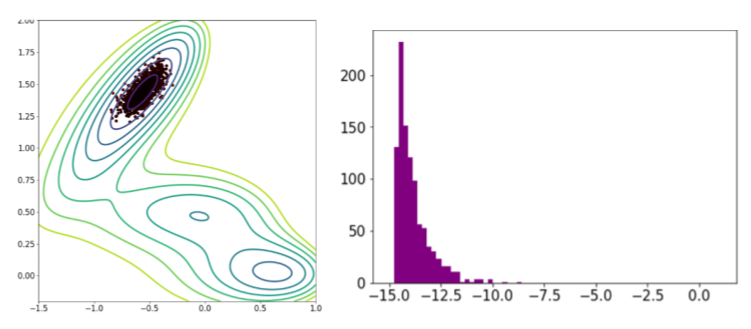
Échantillonnage d’un modèle itératif classique (MCMC) : position des points et distribution en énergie sur le potentiel de Mueller
La simulation à l’ère du Deep Learning
Les méthodes de Deep Learning se sont largement popularisées dans le cadre des modèles génératifs. En règle générale, ces modèles reposent sur une base de données (composée d’échantillons crédibles) et sur des métriques que l’on souhaite optimiser (que l’on appelle fonctions de pertes).
À partir de ces deux éléments, les modèles appréhendent une certaine idée de la distribution sous-jacente de la base de données, et sont capables d’en générer de nouveaux échantillons. Des modèles comme les Réseaux Antagonistes Génératifs (« Generative Adversarial Networks » ou GANs) ou les Auto-Encodeurs Variationnels (Variational Autoencoder ou VAE) qui reposent sur ces techniques sont aujourd’hui démocratisés et largement utilisés.
Dans le cas de la simulation physique, ces techniques apparaissent comme une solution possible pour réduire le temps de calcul. En effet, une fois un tel modèle « entraîné », il est capable d’échantillonner immédiatement des configurations indépendantes sans avoir besoin d’une initialisation et d’itérations (c’est ce qu’on appelle le « one-shot sampling »). Après entraînement, le modèle peut générer quasi instantanément autant d’échantillons que l’on souhaite.
Pourtant leur utilisation en physique reste limitée car ces modèles ne prennent pas en compte certaines contraintes du champ physique.
Tout d’abord leur manque intrinsèque de transparence pose problème dans un univers scientifique où l’objectif est de dégager des lois et d’améliorer la compréhension des phénomènes observés. Pour un physicien, un modèle qui fonctionne mais que l’on ne peut pas expliquer et décomposer a peu de valeur et suscitera de la suspicion.
Ensuite la qualité d’un modèle génératif dépend uniquement de la qualité de sa base de données d’entraînement. Les GANs ou les VAEs sont construits dans l’idée d’être capable de reproduire la distribution de leur base de données d’entraînement. Or la constitution d’une base de données fiable et non biaisée ne va pas forcément de soi.
Enfin, ces modèles sont incapables d’intégrer certains éléments de théorie. Dans le cas des modèles fondés sur l’énergie, on connaît la forme générale de la distribution attendue. On sait que la loi finale satisfait au critère de Boltzmann qui relie la probabilité d’une configuration avec l’énergie de celle-ci : 
où 
est proportionnelle à l’énergie potentielle du système. De même dans le contexte physique, ce n’est pas tant l’échantillonnage général qui est important que la modélisation d’une trajectoire pour laquelle la connaissance des “coordonnées de réaction” peut être utile. Dans les deux cas, ces éléments théoriques sont des indices qui pourraient aider le modèle à être plus pertinent mais qui ne peuvent pas être intégrés dans l’entraînement du modèle.
Pour mettre en lumière ces failles sur l’exemple du potentiel de Mueller, imaginons que l’on cherche à entraîner un VAE. Pour constituer une base de données de départ, on pourrait envisager de lancer une simulation itérative MCMC partant du puits le plus profond (en haut à gauche) puis une seconde partant du puits le moins profond (en bas à droite) afin de constituer une base représentative sur laquelle entraîner le modèle.
Mais après entraînement, le VAE reproduit exactement la base de données sur laquelle il a été entraîné. En particulier, il échantillonne autant de points dans le puits le plus profond que dans le puits intermédiaire, alors même que la physique nous dit que le puits le plus profond (où les énergies sont les plus basses) devrait être sur-représenté.
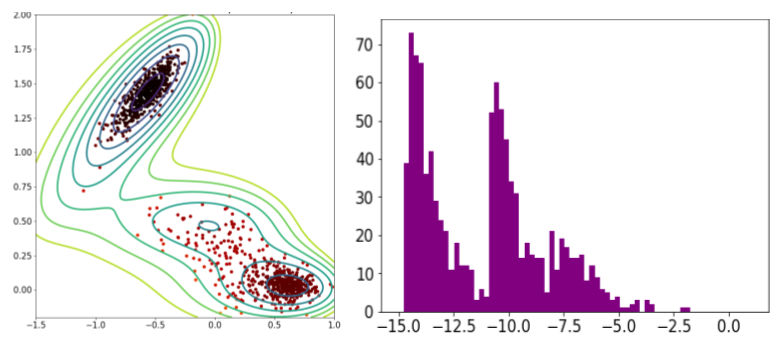
Échantillonnage d’un modèle génératif classique (VAE) : position des points et distribution en énergie sur le potentiel de Mueller
Cette quête d’une plus grande transparence et de la possibilité d’intégrer des éléments théoriques sur les lois échantillonnées pendant l’entraînement conduit à s’intéresser aux réseaux de neurones inversibles (notés par la suite INNs pour « Invertible Neural Networks »).
Les réseaux de neurones inversibles face aux limites des modèles traditionnels
Pour comprendre le changement de paradigme apporté par les INNs, il faut d’abord s’intéresser au fonctionnement des modèles de Deep Learning tels que les GANs ou les VAEs.
Leur principe de base est la recherche d’une fonction de transition entre un espace latent connu et l’espace d’intérêt dans lequel on cherche à échantillonner. On cherche à identifier une fonction qui prendra en entrée des échantillons d’une loi facile à simuler (par exemple une loi Normale) et qui retournera en sortie des échantillons de la loi inconnue qui nous intéresse.
Dans le cas du potentiel de Mueller, on souhaite trouver une fonction capable de prendre en entrée des vecteurs de taille 2 (simulés par une loi normale) et qui renverra des vecteurs de taille 2 représentant la position du point dans l’espace.
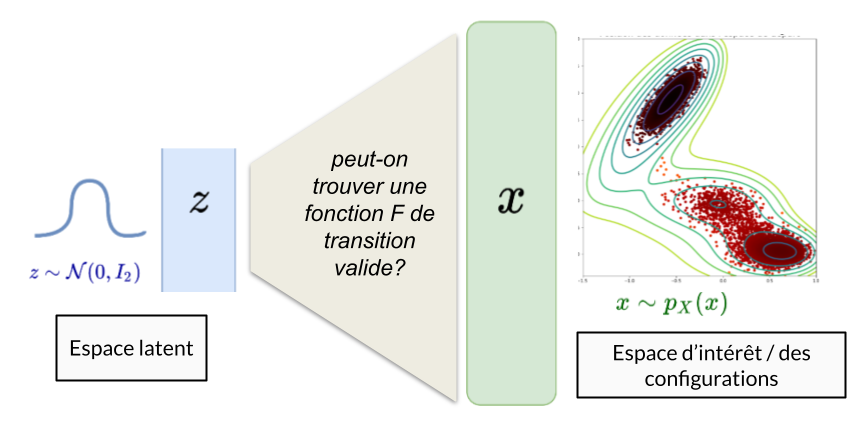
Principe d’un modèle de Deep Learning classique dans le cadre génératif (GAN, VAE)
Le souci réside bien sûr dans le choix de cette fonction de transition F qui doit être suffisamment complexe pour être capable de transformer la Gaussienne et de la modeler en une distribution représentative de notre espace d’intérêt. On a alors recours pour F à un « réseau de neurones », à savoir une succession de transformations (telles que des multiplications par des matrices, l’application de fonctions non linéaires, des convolutions etc). Cette fonction aura de nombreux paramètres (par exemple les poids des matrices) que l’on optimisera grâce à une métrique lors de la phase d’entraînement sur les données.
L’idée de base des INNs est de faire de cette fonction de transition entre espace latent et espace d’intérêt une fonction (1) inversible, (2) bijective, (3) avec des déterminants de Jacobiennes[1] faciles à calculer. Ce sont des contraintes très fortes car les architectures habituellement utilisées pour construire des réseaux de neurones ne respectent pas ces propriétés. En réalité, l’essor récent des INNs n’a été permis que par la découverte du « coupling block » par Dinh et Al [1] : une transformation astucieuse qui permet de garantir l’inversibilité tout en introduisant suffisamment de complexité. C’est à partir de ce bloc de base que sont construits les INNs.
Satisfaire à ces contraintes a deux intérêts principaux :
- Tout d’abord l’introduction d’une bijection entre l’espace latent et l’espace des configurations a intrinsèquement de la valeur. Elle permettra de faire des allers-retours entre ces deux espaces et de percer les rouages de notre modèle grâce à l’analyse de l’espace latent.
- Ensuite la bijectivité de la fonction et la connaissance des déterminants des Jacobiennes permet d’utiliser la formule du changement de variable qui nous donne accès à une expression exacte de la fonction de densité de X (espace des configurations) à partir de celle de Z (espace latent). Cela ouvre la porte à l’utilisation de très nombreuses métriques d’entraînement fondées sur cette fonction de densité : maximum de vraisemblance, divergences avec des lois attendues (comme la loi de Boltzmann décrite dans le paragraphe précédent).
En bref, les INNs permettent une transparence accrue et la possibilité d’intégrer des contraintes théoriques dans l’entraînement du réseau de neurones.
Pour reprendre l’exemple du potentiel de Mueller, il est possible de construire un INN et de l’optimiser selon une panoplie de métriques reposant sur la théorie physique et qui n’étaient pas utilisables avec des architectures classiques. Plus précisément dans cet exemple on peut avoir recours à :
- une métrique « d’apprentissage par l’exemple » : on fournit au modèle des exemples de configurations comme dans un modèle de Deep Learning classique. L’idée est de « cadrer » le modèle en lui donnant un point de départ.
- une métrique « énergétique » : les énergies les plus faibles doivent être surreprésentées et ce en cohérence avec la distribution de Boltzmann.
- une métrique de coordonnée de réaction : comme dans de nombreux cas en physique, on connaît ici une variable collective du système qui nous permet de pousser le modèle à échantillonner le long d’une direction d’intérêt.
À l’issue de cet entraînement, le modèle est capable d’échantillonner de manière indépendante des points dans l’espace, et ce instantanément (plus besoin d’attendre la convergence des méthodes itératives) ; il a également intégré les contraintes énergétiques (la distribution est cohérente avec la loi de Boltzmann) et on peut enfin selon le besoin sur-échantillonner le long d’une coordonnée de réaction, ce qui se révélera très utile pour l’analyse des trajectoires de transition.
Un exemple d’échantillonnage après entraînement est représenté sur la figure suivante. On peut notamment remarquer que la contrainte énergétique est mieux respectée (le puits le moins profond est sous-échantillonné par rapport au puits le plus profond), ce qui n’était pas le cas avec le VAE. D’autre part et sans rentrer dans les détails, la possibilité de passer de l’espace des configurations à l’espace latent (de par le caractère bijectif du réseau) permet d’approfondir la compréhension du problème en analysant la régularité de l’espace latent, voire en procédant à des interpolations.
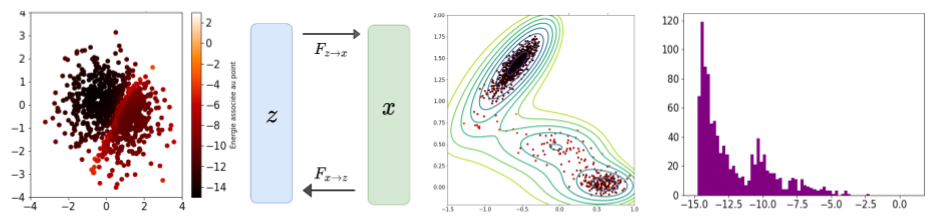
Échantillonnage d’un réseau de neurones inversibles : position des points dans l’espace latent, dans l’espace des configurations, et distribution en énergie sur le potentiel de Mueller
Conclusion : un champ très prometteur mais qui reste encore à défricher !
En conclusion, les Réseaux de Neurones inversibles accélèrent de plusieurs ordres de grandeur les simulations par rapport aux méthodes itératives tout en étant bien plus transparents que les méthodes de Deep Learning du fait de l’inversibilité du réseau.
La recrudescence récente de ces architectures démontre la volonté de la communauté scientifique d’aller au-delà de la précision et de la rapidité de calcul en ajoutant une exigence de transparence et de justesse théorique à l’équation classique de la simulation.
Au sein du laboratoire l’utilisation de cette architecture couplée avec d’autres techniques plus classiques (comme la métadynamique) s’est révélée très prometteuse. Cependant il reste encore quelques points d’interrogation en particulier le passage en très grande dimension et le choix des métriques d’entraînement les plus adaptées.
Affaire à suivre donc …
1 Les Jacobiennes sont une généralisation de la dérivée pour des fonctions vectorielles (avec des espaces d’arrivée et de sortie de dimension supérieure à 1)
Références principales :
[1] Density estimation using Real NVP (Laurent Dinh, Jascha Sohl-Dickstein, Samy Bengio) https://arxiv.org/abs/1605.08803
[2] Boltzmann generators: Sampling equilibrium states of many-body systems with deep learning (Frank Noé, Simon Olsson, Jonas Köhler, Hao Wu) https://www.science.org/doi/10.1126/science.aaw1147
Après un stage de fin d'études de recherches au CEA, Caroline Boudier intègre Dataiku en tant que data scientist.
Commentaires récents