Introduction

Le passé récent a montré que les risques majeurs bouleversent toutes les prévisions et toutes les stratégies. Il a aussi montré qu’au sein même des crises nous sommes souvent démunis, incapables d’envisager correctement les risques dans les risques, c’est-à-dire les possibles évolutions de la crise. Notre futur proche, marqué par le changement climatique, s’annonce aussi difficile, si nous persistons dans des schémas de modélisation qui fonctionnent par analogie avec le passé, et en réalité ignorent en grande partie le risque.

Cet article est une réflexion sur la modélisation des risques. Il est inspiré par plus de quinze ans de pratique dans le domaine des risques opérationnels bancaires, qui n’est bien sûr qu’un sous-ensemble des risques mais couvre, du point de vue des établissements financiers, toutes les catégories comme le risque cyber, les pandémies, le risque géopolitique et le risque climatique, ce dernier étant plutôt un facteur d’exacerbation de risques plus élémentaires.

La Banque des Règlements Internationaux, a bien résumé la difficulté de la modélisation des risques en une seule phrase, dans un document de travail en 2013 : « Risk is, of course, unobservable » [1].

Le point de vue que nous allons développer est simple : les risques étant non observables, on choisit en général d’observer et de modéliser les événements passés, et cette modélisation est pour l’essentiel inadaptée à comprendre les risques et à les envisager de façon rationnelle. Notre pratique nous a montré que la décomposition des risques en mécanismes générateurs d’événements et de conséquences était bien plus féconde que la simple modélisation statistique, celle-ci restant bien sûr essentielle dans certain cas. Les mécanismes sous-jacents à la survenance et au déploiement des risques peuvent être décrits par des enchaînements causaux aléatoires, qui sont bien représentés par les réseaux bayesiens.

Définition du risque

Il est sans doute utile de commencer par une définition du risque, par exemple celle proposée par l’ISO [2], à savoir « l’effet de l’incertitude sur les objectifs ». Cette définition a l’avantage d’être très concise, et en même temps de contenir plusieurs notions importantes : « objectifs », « effet » et « incertitude ».

Il est intéressant de remarquer que la définition ne précise pas si l’effet supposé de l’incertitude est pris en compte lors de la définition des objectifs ou lors de la tentative de réalisation des objectifs. La norme ISO précise dans une note additionnelle « un effet est un écart par rapport à ce qui est attendu », et met ainsi l’accent sur l’exécution plutôt que sur la définition. Nous pensons néanmoins que les deux aspects doivent être pris en compte : l’incertitude perçue peut influencer la définition des objectifs, mais les événements incertains qui se produiront dans le futur auront bien sûr un impact sur la réalisation des objectifs.

Une perception insuffisante des événements potentiels ou des difficultés à venir peut entraîner la fixation d’objectifs irréalistes. La perception des risques doit guider la définition des objectifs et de la stratégie. Cela ne signifie pas qu’une stratégie optimale puisse être définie à partir de l’analyse initiale des risques, mais inversement, une stratégie qui n’est pas informée par une analyse approfondie des risques peut être considérée comme non rationnelle. Cependant, une stratégie non rationnelle, basée sur une intuition ou un pari sur l’avenir, peut toujours être efficace.

Définir le risque comme « un écart par rapport à ce qui est attendu » peut se reformuler en termes mathématiques comme « le risque est la variance de l’objectif autour de sa valeur attendue ». Notons qu’il ne s’agit pas nécessairement d’un objectif financier. L’objectif peut être défini comme un revenu ou un bénéfice mais aussi comme la sécurité, l’impact sur l’environnement, la réputation, etc.

Risque et incertitude

Les incertitudes peuvent être classées selon la dichotomie Known/Unknown, popularisée par Donald Rumsfeld :

  • Les « Known Knowns» sont des certitudes, et sont donc hors du champ de l’incertitude.
  • Les « Known Unknowns», ou les choses dont nous savons que nous ne les connaissons pas. Une partie des inconnus connus peut être traitée à l’aide de probabilités. Ce sont des variables ou des événements identifiés, pour lesquels nous pouvons caractériser notre incertitude. Il s’agit de l’incertitude due aux connaissances inconnues.
  • Les « Unknown Knowns» peuvent sembler contradictoires, mais « les choses dont nous ne savons pas que nous les connaissons » pourraient désigner une connaissance qui nous est accessible, mais pour laquelle nous devons nous engager dans un certain travail pour la rendre explicite – c’est l’incertitude due à la paresse.
  • Enfin, les « Unknown Unknowns» ou « choses dont nous ne savons pas que nous ne les connaissons pas », sont les événements qui ne sont même pas identifiés, comme les perturbations technologiques, les changements géopolitiques, etc.

Il existe une distinction similaire, bien que non équivalente, proposée par Knight. L’auteur de Risk, Uncertainty, and Profit[1] [3] désigne l’incertitude mesurable par le terme risk et conserve le terme uncertainty pour l’incertitude non mesurable. Selon Knight, le profit est le résultat d’une véritable incertitude, alors que la gestion du risque mesurable ne donne lieu qu’à une forme de salaire lié à l’exploitation de la structure du hasard, comme en assurances. « Le profit naît de l’imprévisibilité inhérente et absolue des choses, du fait brut que les résultats de l’activité humaine ne peuvent être anticipés, et ce dans la mesure où même un calcul de probabilité les concernant est impossible et dénué de sens.»

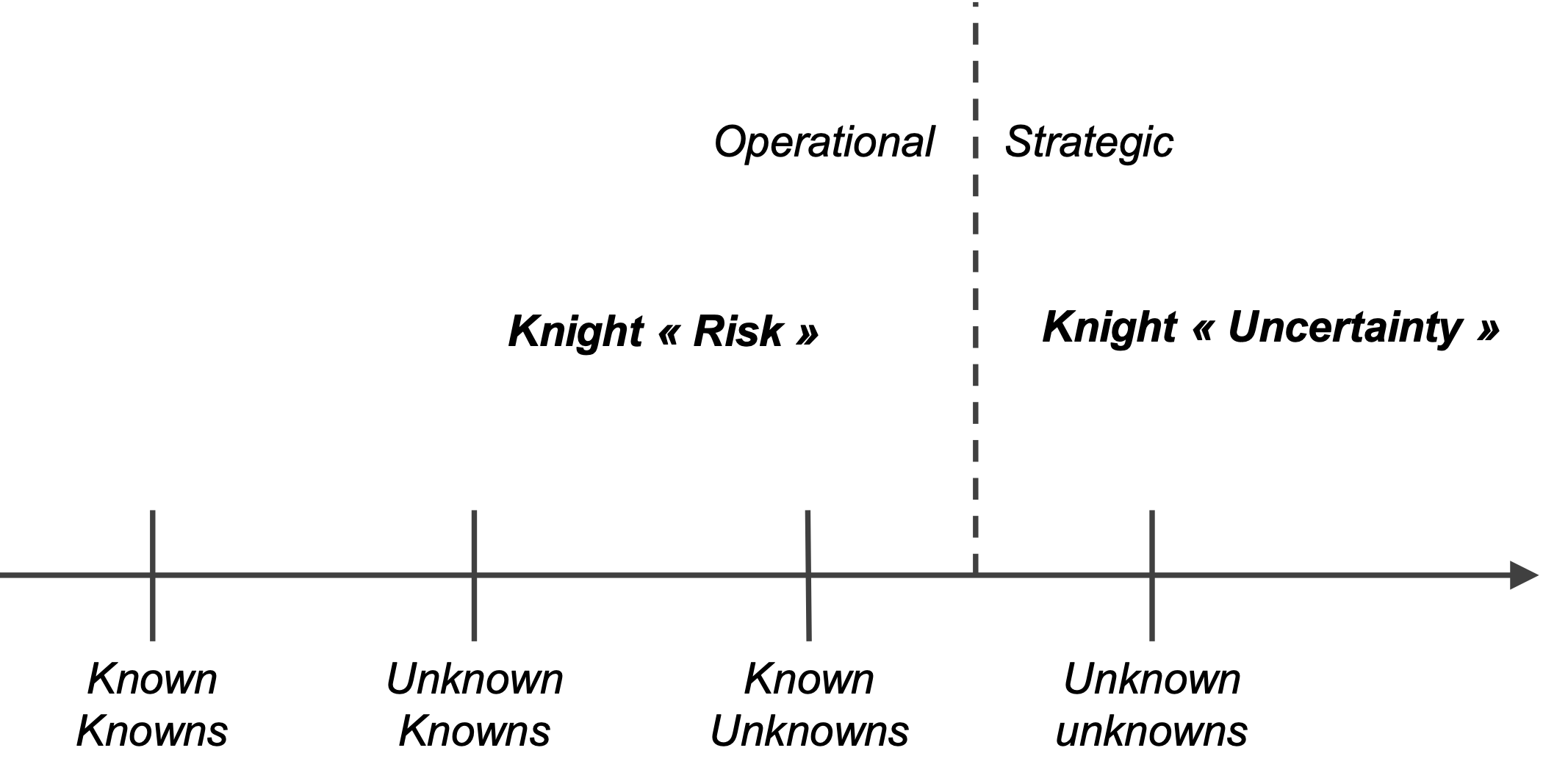
La distinction knightienne entre risque et incertitude ne correspond pas exactement à la distinction entre « Known Unknowns », et « Unknown Unknowns ». En effet, certains Known Unknowns, comme l’issue de certaines tensions géopolitiques, ou le succès de nouvelles technologies, relèvent de la véritable incertitude knightienne.

Méthodes de mesure du risque

Nous discutons à présent de la différence entre l’approche de mesure analytique et l’approche de mesure statistique.

Dans la mesure où le risque est défini comme l’effet de l’incertitude sur les objectifs, nous pouvons en effet soit (1) utiliser des approches statistiques pour évaluer la dispersion autour de l’objectif, soit (2) tenter d’identifier tous les événements possibles qui pourraient avoir un impact sur la réalisation de cet objectif et évaluer leurs conséquences.

En imaginant la réalisation d’un objectif comme un archer visant sa cible, c’est la différence entre, d’une part, l’observation des performances de 1000 archers et l’évaluation de la distance à laquelle la flèche peut s’écarter de la cible et, d’autre part, l’énumération de tous les événements qui pourraient perturber le prochain tir (un coup de vent inattendu, un rayon de soleil, le vol d’un oiseau, etc.).

Dans la plupart des cas, il existe une ligne claire entre ces deux approches : lorsqu’il s’agit de mesurer un risque contrôlable, l’approche analytique est préférable, et lorsqu’il s’agit de mesurer un risque non contrôlable, l’approche statistique est préférable.

Cela s’applique par exemple au risque de projet : un chef de projet essaiera d’identifier tous les risques de son projet, de les mesurer et de les atténuer, tandis qu’un responsable de programme, chargé d’un portefeuille de projets, préférera utiliser une approche statistique pour chaque projet.

Dans le domaine bancaire, il en va de même pour le risque de crédit. Le défaut des emprunteurs n’étant pas un risque directement gérable par la banque, les probabilités de défaut seront évaluées statistiquement. Mais le niveau de risque du portefeuille global peut être géré par une allocation rationnelle, en tenant compte des différentes probabilités de défaut, et des corrélations entre les défauts.

Bien sûr cela s’applique également au risque de marché. La distribution des rendements du marché n’est pas quelque chose qu’une banque peut contrôler, mais elle peut concevoir une structure de portefeuille appropriée pour optimiser le rapport risque/rendement.

On voit qu’en général il y a une opposition entre gérer les risques et les mesurer statistiquement : La mesure statistique du risque exprime un renoncement à sa gestion.

On peut considérer que c’est cette opposition que Louis Bachelier a formalisée en 1900 dans sa  Théorie de la spéculation  [4]. Suivant l’hypothèse selon laquelle les rendements boursiers sont imprévisibles, en raison des innombrables facteurs qui influencent l’opinion des investisseurs, Louis Bachelier déduit mathématiquement l’une des idées les plus importantes du monde de la finance, à savoir que les rendements des cours sont normalement distribués (ce que la plupart des non-mathématiciens trouveraient mystérieux).

Les facteurs qui influencent la variation des prix des actions sont impossibles à énumérer et à quantifier, mais ils sont, à un niveau général, similaires pour différents titres. Par conséquent, un gestionnaire de portefeuille ne comprend pas ce qui motive les mouvements de prix des différentes actions de son portefeuille, mais cela ne l’empêche pas de gérer les risques de son portefeuille en optimisant son allocation. Cette approche est similaire à celle d’un gestionnaire de portefeuille de projets qui n’a pas le contrôle des projets individuels et qui traite le risque de chacun d’entre eux de manière statistique, tout en essayant de contrôler le risque global de son portefeuille.

Mais dans les deux cas, le gestionnaire d’un projet particulier doit gérer les risques identifiés de son projet, et le dirigeant d’une société cotée en bourse doit gérer les risques qui peuvent affecter sa valeur marchande.

Autrement dit, une approche de mesure purement statistique est adaptée si le risque est mesuré pour une entité considérée comme échappant au contrôle du gestionnaire de risques. Lorsque le gestionnaire de risques gère efficacement les risques – d’une entreprise, d’un projet, d’un portefeuille d’actifs ou d’un portefeuille de projets – l’approche appropriée est l’approche analytique.

Les réseaux bayesiens

Dans son essai historique publié à titre posthume (Essay Towards Solving a Problem in the Doctrine of Chances, 1763) [5], Thomas Bayes a introduit à la fin du 18° siècle deux notions essentielles dans la théorie de la décision.

D’une part, selon Bayes, c’est le prix P que je suis prêt à payer pour pouvoir bénéficier du gain R que m’offrirait la survenance d’un événement incertain, qui définit la probabilité de cet événement comme valant P/R.
D’autre part, il définit la notion de probabilité conditionnelle, mettant en évidence le fait que la probabilité d’un événement à venir et incertain dépend du niveau d’information dont on dispose avant la survenue de cet événement. Cette notion est fondamentale car elle exprime le fait que l’incertitude est spécifique à chacun en fonction de son niveau de connaissance, et est donc plus proche d’une « croyance » (belief en anglais) que d’une fréquence.

En formalisant le lien intuitif entre « information » et « probabilité », ou autrement dit entre « connaissance » et « non-connaissance », Bayes pose ainsi les bases de toute théorie de la décision. La décision rationnelle est celle qui recherche toute l’information disponible – décider en connaissance de cause.

Conçus par Judea Pearl dans les années 1980 [6], les réseaux bayesiens [7] sont des modèles causaux probabilistes. Un réseau bayesien est constitué d’un graphe dérivant les dépendances causales entre les variables et d’une distribution de probabilités décrivant l’incertitude résiduelle de cette dépendance. Le graphe représente donc la structure de la connaissance, et les probabilités représentent la partie incertaine du domaine.

Utilisation en gestion des risques

Explicitons cette idée sur un exemple très simple en gestion des risques [8].

Un opérateur travaillant sur une machine risque de se blesser, s’il l’utilise mal. Ce risque dépend de l’expérience de l’opérateur et de la complexité de la machine. «Expérience» et «Complexité» sont deux facteurs déterminants de ce risque.

Bien sûr, ces facteurs ne permettent pas de créer un modèle déterministe. Si l’opérateur est expérimenté, et la machine simple, cela ne garantit pas qu’il n’y aura pas d’accident. D’autres facteurs peuvent jouer : l’opérateur peut être fatigué, dérangé, etc. La survenance du risque est toujours aléatoire, mais la probabilité de survenance dépend des facteurs identifiés.

Le schéma ci-dessous représente la structure de causalité de ce modèle (graphe).

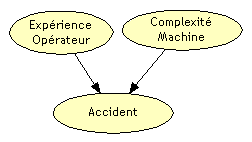
Ce graphe peut être complété par des tables de probabilité. La table la plus importante est celle qui exprime la dépendance de l’accident à l’expérience de l’opérateur et à la complexité de la machine.

– Table de probabilités conditionnelles (en %) –

On comprend bien ici que la connaissance est partielle. Si l’utilisateur est expérimenté et la machine simple, il n’y aura sans doute pas d’accident (0,1% de chances dans l’exemple ci-dessus). Mais le fait de conserver une probabilité résiduelle reconnaît le fait que tous les facteurs de risque ne sont pas pris en compte dans ce modèle.

Le réseau bayesien représente donc à la fois la connaissance et la non-connaissance du domaine. Ce qui est connu est représenté par la structure de causalité (le graphe). Ce qui n’est pas connu est matérialisé par des probabilités.

Le réseau bayesien exprime finalement, et simplement, que l’expérience de l’opérateur et la complexité de la machine influent sur la probabilité d’un accident. C’est précisément le sens de l’approche de Thomas Bayes : la probabilité dépend du contexte.

Utilisation en communication sur les risques

La pandémie de Covid a contribué à vulgariser la notion de modèles, qui étaient utilisés pour fonder les décisions gouvernementales.

En matière de gestion des risques, la transparence des modèles nous semble essentielle, puisque précisément l’objet d’étude n’est pas observable. Un modèle graphique, décrivant les hypothèses de causalité et les hypothèses de probabilité, peut s’avérer très utile pour initier une discussion critique et constructive. Pour illustrer ce point, nous présentons justement un modèle de stratégie de prévention et de protection face à une pandémie [9]. Cette étude a été effectuée dans le cadre de la réflexion sur les pandémies qui a été lancée dans les années 2000 après les craintes suscitées par la grippe H1N1.

Ce modèle permet de représenter d’une part les variables régissant le coût de la contamination d’une personne sous forme d’un réseau bayesien, et d’autre part les stratégies d’intervention.

 

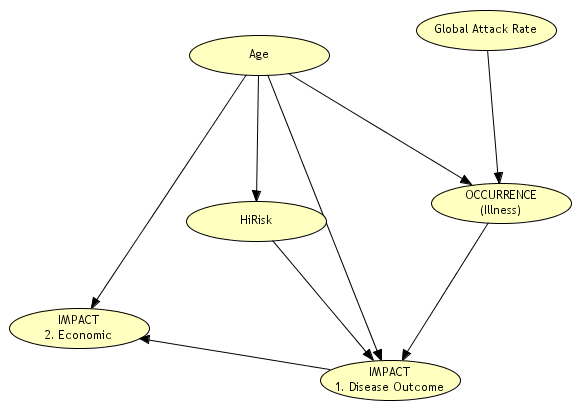
Ce graphe représente pour une personne exposée la possibilité de survenance, c’est-à-dire la contamination, et l’impact, c’est-à-dire les conséquences de la maladie.

La survenance dépend d’une variable appelée le taux d’attaque global qui formalise la fraction de la population sensible au virus. Les taux d’attaque considérés pour une pandémie varient entre 15 % et 35 %, voire 50 % pour certains auteurs.

Conditionnellement à ce taux d’attaque, la probabilité de contamination dépend aussi de l’âge. Elle peut être donc représentée par une table de probabilité conditionnelle à deux « causes » similaire à celles détaillées dans l’exemple précédent

Pour une personne contaminée, les conséquences peuvent être de trois types : soins à domicile, hospitalisation, ou décès. Le type de conséquence dépend de l’âge et de l’appartenance à un groupe à risque, comme le graphe permet de le visualiser. L’estimation quantitative de la probabilité de chaque type de conséquence en fonction de l’âge et de l’appartenance à un groupe à risque (HiRisk dans le graphe) peut être basée sur des cas passés, avec un degré d’incertitude, et être affinée à mesure que les informations sur la maladie sont actualisées. Comme précédemment, ces dépendances seront représentées par des tables de probabilité conditionnelles.

Une fois ce modèle établi, la structure d’une population particulière conditionne donc les conséquences. On a bien sûr vu l’influence de cette structure pendant la crise du Covid, en comparant l’impact de la pandémie sur les populations africaines jeunes et en bonne santé, et les populations occidentales, vieillissantes et souvent en surpoids, notamment aux Etats-Unis.

La deuxième étape est de représenter la stratégie de réponse à la pandémie sur le même graphe.

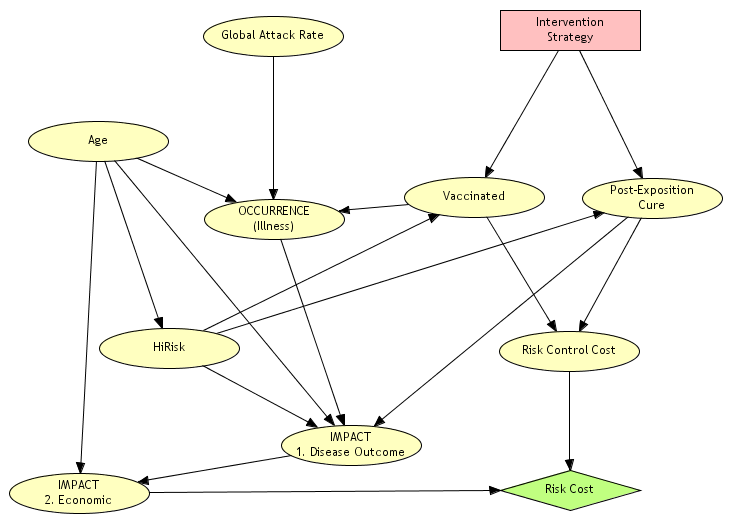
La représentation de la stratégie est obtenue en ajoutant au graphe initial quatre nœuds :

  • Une variable représentant la stratégie d’intervention, figurée par un rectangle
  • Une variable représentant le statut vaccinal d’une personne
  • Une variable représentant les soins post-exposition administrés à une personne
  • Une variable représentant le coût du risque, figurée par un losange

La stratégie détermine le statut vaccinal et le traitement d’une personne en fonction de son âge et de son niveau de risque. Cette stratégie peut être de vacciner toute la population, de vacciner seulement les personnes à risque, ou bien encore de traiter l’ensemble des personnes, ou uniquement les personnes à risque.

Chaque stratégie a un coût direct qui est celui de sa mise en œuvre (vaccins, traitements), mais également un coût indirect représentant les conséquences évitées ou non évitées sur les patients. L’utilité d’une stratégie est définie par son coût total incluant les coûts de prévention et de protection, ainsi que le coût des soins résiduels. Cette utilité est représentée dans la variable en forme de losange.

Avec un tel modèle, les stratégies peuvent donc être comparées en termes d’utilité – ce qui n’est pas nécessairement pertinent dans une optique de « quoi qu’il en coûte » mais peut s’avérer très utile si les ressources, et notamment les vaccins et les traitements, sont limitées.

Notre propos n’est pas ici de présenter un modèle pour gérer une pandémie, mais bien d’illustrer la puissance de communication de tels modèles. Ces graphes peuvent être présentés, sinon au grand public, du moins à un large public. Ils peuvent être discutés, remis en question et améliorés par des échanges entre experts. Ils peuvent intégrer les nouvelles connaissances disponibles rapidement.

Utilisation pour le benchmarking

La modélisation des risques est, nous l’avons dit, la représentation d’une perception plutôt que d’un objet observable. Au sein d’une organisation, ces perceptions font souvent l’objet de biais et de déformations, volontaires ou non. Dès lors, la comparaison avec ses pairs est un outil puissant pour identifier ces biais et les corriger, mais aussi pour identifier et corriger les éventuelles lacunes de l’organisation.

Dans notre domaine d’application, c’est-à-dire la modélisation des risques opérationnels bancaires, nous menons depuis plusieurs années un projet de recherche sur ce sujet, en particulier dans le domaine du risque cyber [10].  Un groupe de huit banques américaines a travaillé sur neuf scénarios de risque cyber, afin d’arriver à une représentation commune permettant une comparaison ultérieure des hypothèses. Les neuf scénarios ont été définis en considérant les combinaisons significatives entre les trois dimensions Assets, Access, Attacker, autrement dit en se demandant quel type d’attaquant attaque quelle type de ressource, et par quel type d’accès. Dans le graphe en forme de roue ci-dessous, cela revient à considérer toutes les combinaisons possibles et à retenir les plus pertinentes.

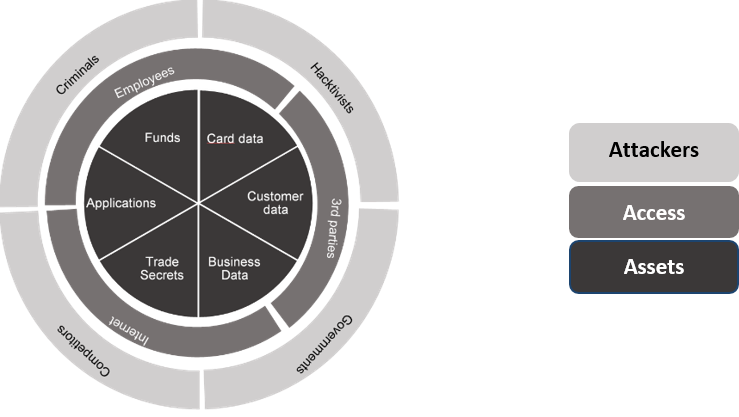
Puis, pour chaque scénario, les participants se sont mis d’accord sur une structure commune du réseau bayesien, qui représente le mécanisme de génération des événements et des conséquences associées. La figure ci-dessous présente l’une des structures retenues pour un scénario de cyber attaque sur une application critique.

 

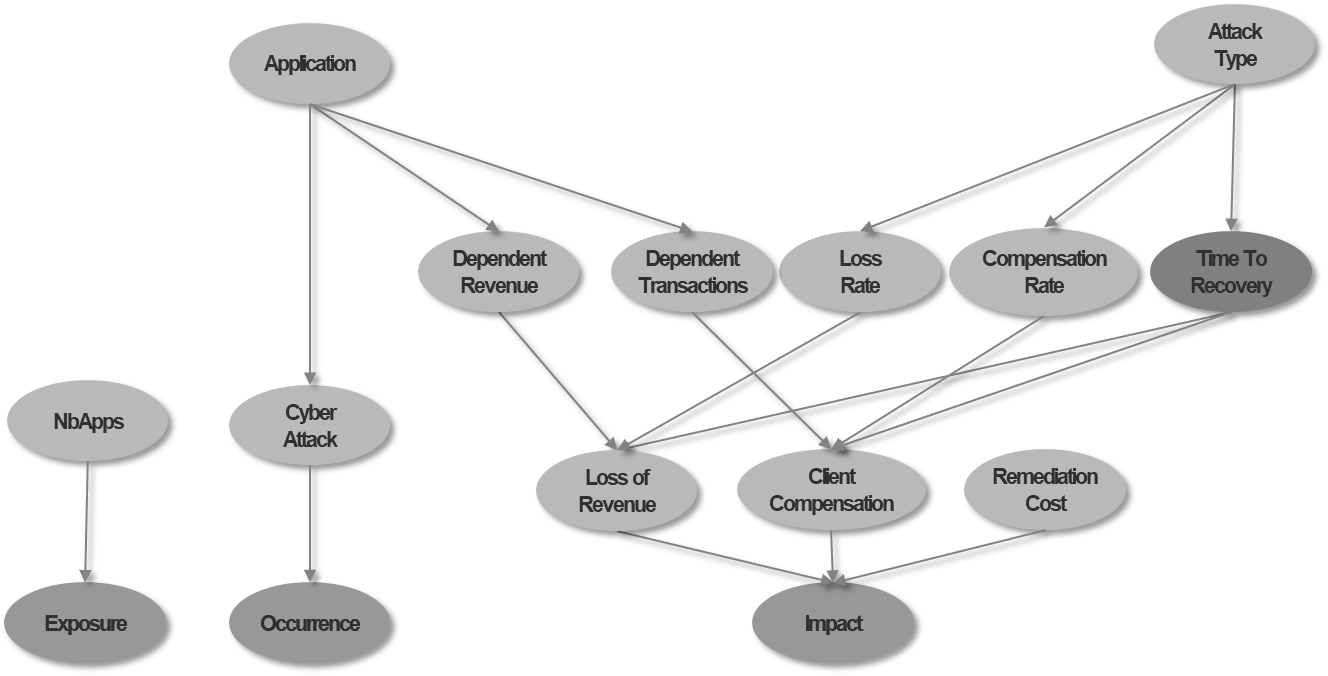
En ce qui concerne les hypothèses quantitatives, un point de départ était proposé, et chaque banque fournissait sa propre estimation. Il est important de signaler que la confidentialité des hypothèses formulées était garantie. Chaque banque avait accès à l’ensemble des hypothèses formulées par ses pairs de façon anonyme.

Cette expérience a permis d’améliorer l’approche du risque cyber au sein des établissements participants, ce risque étant souvent considéré comme grave mais difficile à estimer. Parmi les enseignements tirés de cette recherche, les participants ont considéré que la collecte des données et des avis d’expert était grandement facilitée par l’existence d’une structure a priori, qui permet une définition très précise de chaque variable.

Pour certains scénarios, la dispersion entre l’évaluation des risques extrêmes pouvait aller de 1 à 10, après mise à l’échelle par la taille de l’établissement, bien sûr. L’impact de chaque scénario était évalué en jours de revenu, ce qui permet une mise à l’échelle naturelle. La dispersion s’expliquait selon les cas, soit par des différences d’organisation, soit par la différence de perception de la qualité des contrôles. Là encore, la structuration du scénario a permis de bien isoler les aspects les plus subjectifs de l’évaluation, afin de si possible les rendre plus objectifs et mesurables

Conclusion

La reconnaissance de la nature subjective de l’évaluation des risques est selon nous un pas essentiel à leur meilleure maîtrise. Comme la crise des subprimes en 2008 l’a montré, utiliser des modèles, c’est d’abord y croire. Y croire, c’est parfois se tromper. Plus les modèles sont opaques et difficiles à communiquer, et plus le risque d’aveuglement lié à une croyance érigée en vérité scientifique est élevé.

La crise qui est devant nous, et qui est liée au changement climatique, est probablement celle qui fait l’objet d’un des efforts de modélisation les plus importants de tous les temps. Le GIEC a eu l’intelligence de faire apparaître dans chacune de ses affirmations la notion de consensus et la notion de fiabilité. Ainsi, le caractère subjectif et faillible des modèles est mis en avant. Cependant il reste selon nous beaucoup d’efforts à faire pour faire comprendre au public – et même aux décideurs politiques – les enchaînements de causalité à l’œuvre, en particulier en ce qui concerne les points de bascule entraînant des rétroactions positives. L’utilisation de réseaux bayesiens serait parfaitement adaptée à cette représentation.

En même temps que le changement climatique se manifeste, entraînant avec lui un probable déplacement de l’état d’équilibre de notre planète, et bien sûr un changement profond de nos habitudes et de nos comportements, le monde développé semble entré dans une frénésie de « big,data », considérant urgent d’exploiter des masses de données bientôt obsolètes, pour en tirer des règles et des modèles qui le seront aussi.

Notre conclusion sera celle de Judea Pearl, l’inventeur des réseaux bayesiens, qui affirme dans son livre récent The Book of Why [12] : « Les questions de causalité ne peuvent jamais être décidées par les données seulement. Il nous faut d’abord formuler un modèle du processus générateur des données ».

 

Mots-clés : bayesien – risque – Knight – incertitude – mesure

 

[1] Voir la note de lecture de A. Charpentier dans https://variances.eu/?p=6028.

Références

[1] – Basel Committee on Banking Supervision. Discussion Paper BCBS258 “The regulatory framework: balancing risk sensitivity, simplicity and comparability” July 2013. https://www.bis.org/publ/bcbs258.pdf

[2] – ISO 31000:2018 Risk management — Guidelines. https://www.iso.org/standard/65694.html

[3] – Knight, Frank, D., Risk, Uncertainty and Profit, 1921 https://fraser.stlouisfed.org/files/docs/publications/books/risk/riskuncertaintyprofit.pdf

[4] – Bachelier, L. (1900), « Théorie de la spéculation », Annales Scientifiques de l’École Normale Supérieure.

[5] – Bayes, Thomas, An Essay Towards Solving a Problem in the Doctrine of Chances, 1763 https://royalsocietypublishing.org/doi/pdf/10.1098/rstl.1763.0053

[6] – Pearl, Judea Probabilistic Reasoning in Intelligent Systems : Networks of Plausible Inference, Morgan Kaufmann, 1988, 552 p.

[7] – Naïm, Patrick ; Wuillemin, Pierre-Henri ; Leray, Philippe ; Pourret, Olivier ; Becker , Anna, Réseaux bayesiens, Eyrolles, 2011, 3e éd., 424 p.

[8] – Cet exemple est repris du livre « Risk Quantification », (Condamin, Louisot, Naïm, Wiley 2006) également utilisé dans la page française de Wikipedia sur les réseaux bayesiens.

[9] – Cet exemple est repris du livre « Risk Quantification », (Condamin, Louisot, Naïm, Wiley 2006)

[10] – Condamin, Laurent; Marie, Clémentine; Naïm, Patrick, A pilot project for peer benchmarking of operational risk scenarios, Journal of Risk Management in Financial Institutions, Volume 11, Number 4, 2018.

[11] – IPCC – Sixth Assessment Report (2022) https://www.ipcc.ch/assessment-report/ar6/

[12] – Pearl, Judea; Mackenzie, Dana (2018). The Book of Why, The New Science of Cause and Effect, Basic Books, New York. https://www.basicbooks.com/titles/judea-pearl/the-book-of-why/9780465097616/

Patrick Naim
Les derniers articles par Patrick Naim (tout voir)