Variances présente ci-dessous deux textes d’ex-Insee sur les sondages préélectoraux. Le premier rappelle, s’appuyant sur l’histoire ancienne, les conditions méthodologiques pour obtenir de bons sondages. Le second, sorte d’illustration du premier basée sur l’histoire récente, semble considérer que ces méthodes sont maintenant bien maîtrisées.
Le vote de paille, 86 ans plus tard
Jean-François Royer
Jean-François Royer a fait toute sa carrière à l’INSEE où il a été notamment chef du département de l’action régionale. Il est retraité depuis 2010 et s’est investi dans le groupe « Statistique et enjeux publics » de la Société française de statistique.
Que valent les sondages pré-électoraux publiés par les instituts spécialisés ? On va se poser la question encore une fois en 2022. L’expérience des « votes de paille »[1] américains du début du XXe siècle a-t-elle quelque chose à nous dire à ce sujet ?
Ces « votes de paille » sont restés célèbres à cause de leur débâcle en 1936. C’était une sorte d’institution depuis 1916 : la revue « Literary Digest » (LD) les organisait avant chaque élection présidentielle en adressant, par voie postale, des pseudo-bulletins de vote à un large échantillon[2] d’électeurs, et en dépouillant les retours. Lors des élections de 1928 et 1932, ces opérations avaient permis à la revue de prédire correctement le résultat. En 1936, l’échantillon constitué à partir d’annuaires téléphoniques, de listes électorales, de listes de membres des clubs automobiles, etc. atteignit la taille de dix millions de bulletins, parmi lesquels 2,4 millions furent remplis et retournés à la revue. Fort de quoi, le LD annonça fin octobre une nette victoire du challenger républicain Alfred Landon sur le président sortant F.D. Roosevelt. Pourtant, en novembre 1936, ce fut Roosevelt qui gagna l’élection, avec une marge confortable sur Landon. Et ce fut la fin des « votes de paille » !
L’échec du LD n’a pas cessé d’être analysé depuis : on peut sans exagérer le qualifier de « moment fondateur des sondages d’opinion modernes ». 86 ans plus tard, au moins trois leçons de portée générale peuvent être proposées.
Première leçon : tous les segments importants de la population doivent être justement représentés dans l’ensemble des répondants
L’échec de 1936 fut analysé dès 1937-1938, notamment par Georges Gallup, qui avait prédit le bon résultat en s’appuyant sur un échantillon de seulement 50 000 électeurs. C’est la composition de l’échantillon du LD qui fut alors jugée cause principale de l’erreur : les listes utilisées contenaient trop d’électeurs des catégories sociales aisées, qui votaient plus souvent Républicain que Démocrate. Le recours aux annuaires téléphoniques et aux registres des clubs d’automobile fut particulièrement incriminé, téléphone et automobile étant peu répandus à l’époque, même aux États-Unis. Pour que les comptages soient fiables, tous les segments importants de la population doivent être représentés dans l’échantillon interrogé, et dans l’ensemble des répondants, proportionnellement à leur présence dans la population.
C’est cette idée qui nous amène à ériger comme un idéal le « sondage aléatoire » dans lequel chaque votant a une probabilité non nulle a priori d’appartenir à l’échantillon, et qui est construit à l’aide d’un hasard contrôlé. Théoriquement, en l’absence de non-réponse, cette procédure garantit la représentation de tous les segments, de quelque manière qu’on les définisse : sexes, âges, catégories sociales, tendances politiques, etc. Pour diverses raisons, économiques en particulier, elle n’est pas applicable pour les sondages préélectoraux : les instituts de sondages qui réalisent ceux-ci ont recours à des méthodes de désignation de leurs échantillons plus empiriques, même si le tirage au sort y joue parfois un rôle. L’utilisation de quotas par sexe, âge, catégorie sociale permet d’atteindre une juste représentation des catégories correspondantes, mais quid d’autres critères ? Des inégalités de représentation ne sont-elles pas à craindre selon l’orientation politique, le degré de familiarité avec les médias, l’aptitude à utiliser Internet ? Seul un examen critique précis d’un processus d’échantillonnage peut détecter les éventuelles failles, et permettre d’en évaluer les risques. Il faudrait que les instituts de sondages se livrent eux-mêmes en permanence à ce genre d’examen ; d’autres pourraient le faire aussi, à condition de disposer des informations suffisantes. Malgré le légitime « secret des affaires », une obligation accrue de « transparence » ne serait-elle pas nécessaire ? En France, c’est la « commission des sondages » qui est chargé de réguler l’activité des instituts de sondage dans le domaine politique ; on pourra se reporter à son communiqué du 11 mars 2022[3].
Deuxième leçon : les redressements, ça aide !
Le vote de paille de 1936 continue à être étudié par des chercheurs américains. Il faut dire que des données détaillées avaient été publiées à l’époque par LD, et peuvent être exploitées de nouveau. Dans un article paru en 2017 (référence in fine) deux statisticiens présentent le résultat d’une « repondération » du vote de paille. Le pseudo-bulletin de vote incluait une rubrique « Indiquez comment vous avez voté à l’élection présidentielle de 1932 ». Et les résultats publiés par LD en octobre 1936 permettent d’exploiter cette rubrique : pour chaque État, et chaque intention de vote 1936, on dispose de la répartition des souvenirs de votes de 1932[4]. Ces données permettent de « redresser » les votes de paille 1936 provenant d’un État de façon que la répartition politique des souvenirs de vote 1932 devienne conforme aux résultats effectifs des élections de 1932 dans cet État. Eh bien, la prédiction est alors renversée : ainsi repondéré, le vote de paille prédit la victoire du président sortant, et non plus celle de son challenger[5] (d’où le titre que les deux statisticiens ont donné à leur article). L’inversion n’est pas complète, le résultat est encore assez loin du résultat 1936 effectif, mais le renversement est bien là ; et le calcul aurait pu être fait dès octobre 1936, méthodes et données étant disponibles dès cette date. Le LD aurait ainsi évité sa débâcle : mais il a préféré ne pas le faire, et pour sa défense a donné après coup un argument qu’on rencontre encore aujourd’hui : « Nous n’avons pas tenté d’interpréter les chiffres, parce que notre seul enjeu par rapport au résultat était notre souhait de préserver notre réputation bien gagnée de comptables scrupuleux » … Fascination des « résultats bruts ».
La méfiance vis-à-vis des redressements demeure, alors qu’ils sont indispensables. Même si aucun segment de la population ne manque dans l’échantillon, le pourcentage de non-réponse peut différer fortement selon les catégories, et notamment selon l’orientation politique. Il est donc légitime de faire en sorte que l’ensemble répondant ressemble du mieux possible à la population, aussi bien selon les critères socio-démographiques que selon l’orientation politique, pour autant que celle-ci puisse être mesurée objectivement. Et pour cela, les résultats d’élections précédentes sont irremplaçables.
Troisième leçon : plus gros ne veut pas toujours dire plus sûr, encore que …
Présenter des résultats reposant sur plus de deux millions de bulletins, cela pesait lourd en 1936 pour emporter la conviction. Ébranler cette confiance mal placée a certainement été une des conséquences les plus importantes du fiasco. Pour autant, faisons-nous toujours un bon usage de l’information qu’on nous donne sur la taille des échantillons ? On peut en douter.
En présence d’un sondage aléatoire, les statisticiens peuvent chiffrer l’ordre de grandeur des « erreurs d’échantillonnage », celles qui sont imputables au seul fait qu’on n’interroge pas la totalité de la population. Ces marges d’erreur diminuent quand la taille de l’échantillon augmente, comme on pouvait s’y attendre. « Plus gros » veut donc quand même dire « plus sûr », de ce point de vue. Mais la précision augmente moins vite que la taille[6].
La pratique s’est généralisée de mettre en avant des chiffrages des erreurs d’échantillonnage même pour des enquêtes qui ne sont pas aléatoires : on les calcule « en faisant comme si » on avait à traiter les résultats d’un sondage aléatoire simple de même taille que l’enquête examinée. Par exemple, lorsqu’une enquête par quotas ayant récolté 1 000 questionnaires indique : « le candidat A recueille 20 % des suffrages », on assortit ce résultat d’une « marge d’erreur d’échantillonnage de 2,5 % en plus ou en moins »[7] comme si on avait affaire à un échantillonnage aléatoire de 1 000 personnes dans sa forme la plus simple.
Cette pratique est sans doute utile, notamment pour alerter les lecteurs lorsque des indicateurs sont calculés sur des échantillons de très petite taille. Mais on peut la juger contre-productive. Dans certains cas, elle peut exagérer la marge d’erreur d’échantillonnage, que des redressements ont pu diminuer. Mais surtout, dans tous les cas, elle risque de masquer aux yeux d’un public peu averti les autres risques d’erreur, comme ceux qui ont plombé le « vote de paille » de 1936 : autres risques que ces calculs n’ont aucune vocation à prendre en compte.
Aucun sondage n’étant rigoureusement aléatoire, rien ne peut remplacer l’examen soigneux de la totalité du processus d’échantillonnage, d’enquête et de redressement !
Lohr, Sharon L. , Brick J. Michael « Roosevelt predicted to win : Revisiting the 1936 Literary Digest Poll » Statistics, Politics and Policy, De Gruyter 2017 ; vol. 8(1) pages 65-84
Faut-il croire les sondages au premier tour d’une présidentielle ?
Pierre Joly (ENSAE 1978)
Il serait présomptueux de répondre à cette question pour les élections actuelles avant le 10 avril au soir. Certes de nombreux sondages convergent sur les résultats des différents candidats sans que l’on puisse préjuger de la part qui pourrait revenir à un certain mimétisme.
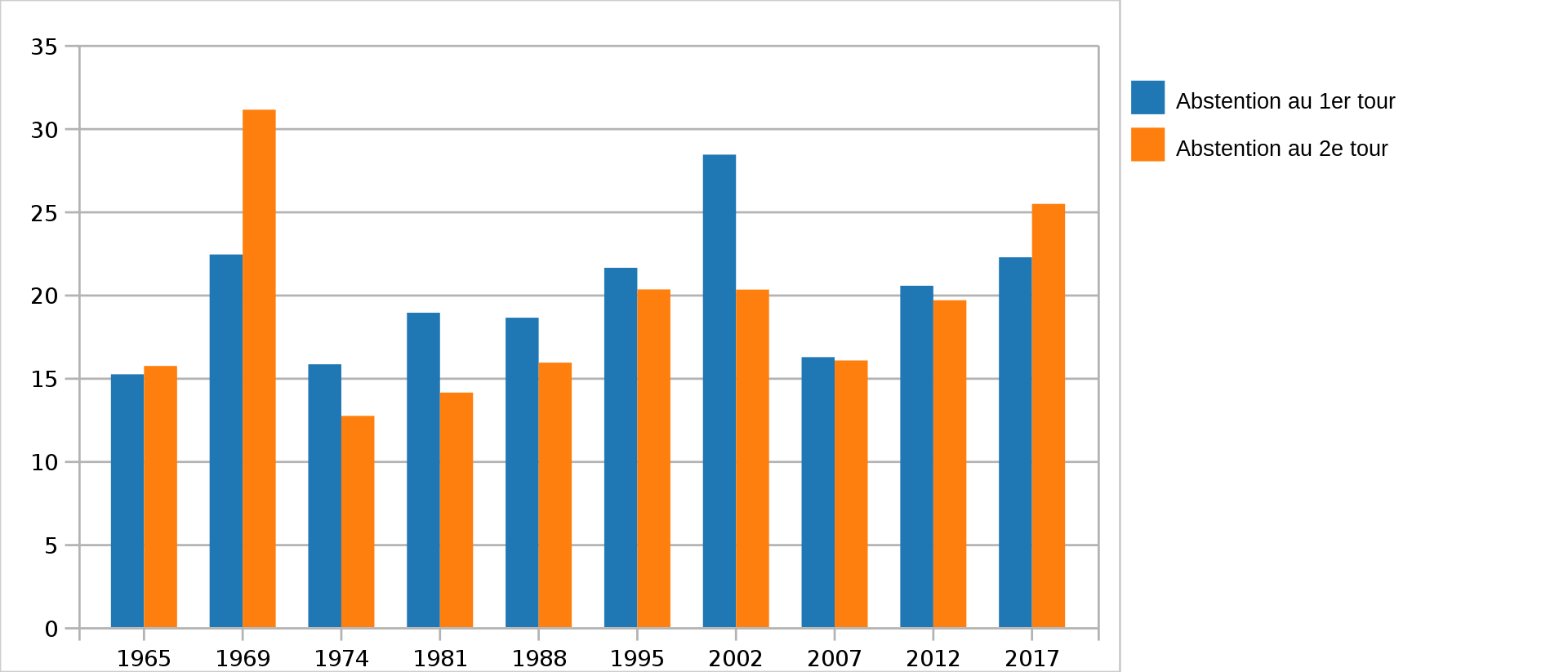
Toutefois, la prévision d’un fort taux d’abstention voisin de 30% est assez inédite. Seules les élections de 2002 ont connu un taux voisin (28,4%). La surprise du résultat final avec la qualification de Jean-Marie Le Pen et l’échec de Lionel Jospin a conduit beaucoup d’électeurs, surtout de gauche, à se sentir trahis par les prédictions des sondages. Il est vrai que le contexte sociétal de la dernière semaine avait favorisé les candidats de droite qui avaient presque tous gagnés des points et que l’électorat de gauche s’était éparpillé sur 9 candidats et la droite sur 7 seulement. La baisse de deux points de Lionel Jospin et la remontée de 2 à 3 points de Jean-Marie Le Pen ont eu raison des pronostics des sondages qui annonçaient un duel serré entre le Jacques Chirac et Lionel Jospin donnés à égalité pour le second tour.
Que nous enseignent les sondages portant sur le premier tour de l’élection présidentielle de 2017 ? Il s’agissait pourtant d’une élection peu ordinaire. Le président sortant ne se sentait plus en position de se présenter avec son parti assez divisé. Le favori se trouvait mis en difficulté par des affaires portées en justice et un nouveau venu se présentait en créant son mouvement en grande partie fondé sur la société civile. Étonnamment pourtant, on a constaté que les instituts de sondage ont prédit avec justesse les résultats du premier tour et en particulier pour les trois candidats arrivés en tête.
Si on calcule une distance quadratique entre chaque sondage réalisé à partir du 18 mars 2017, soit 36 jours avant les élections du 23 avril 2017, on constate une réduction sensible dans le temps de cette distance jusqu’à une stabilité sur les dix derniers jours.
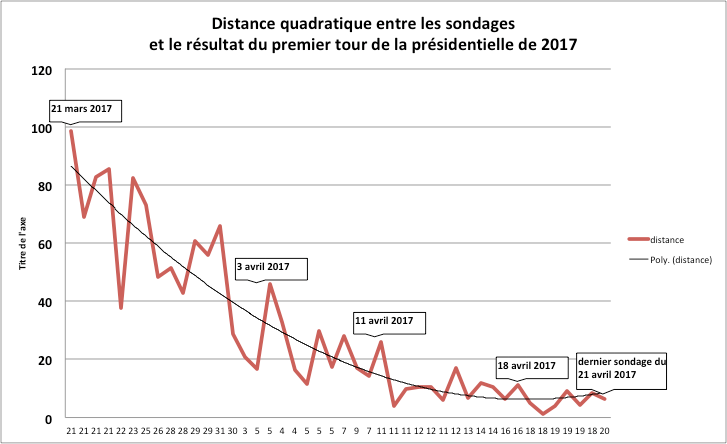
Le résultat du premier tour a été celui prédit pour Emmanuel Macron à 24%, plus favorable de 0,3 points pour François Fillon à 20%. Il a été meilleur pour Jean-Luc Mélenchon de 0,5 points à 19,6%, mais plus défavorable pour Marine Le Pen avec 21,3% à presqu’un point en dessous des derniers sondages.
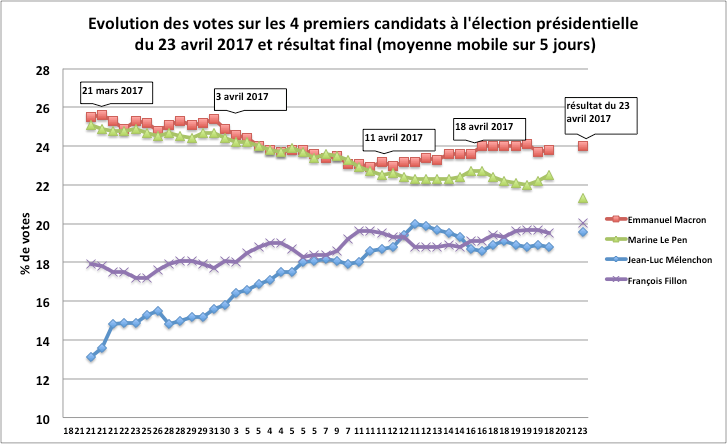
Les prévisions pour 2022 sont toutefois différentes puisque les trois premiers candidats présentent des écarts significatifs avec 5 à 7 points entre les deux premiers et autour de 6 points entre le deuxième candidat et le troisième. Ceci pourrait-il conduire à valider les prévisions des sondages sur les deux premiers ? Probablement sauf si la dernière semaine de présentation des candidats leur permet d’amener plus d’électeurs aux urnes.
Pour prolonger ces analyses il est possible de se reporter à trois articles du bien utile site wikipedia qui ont servi de sources à cet article :
Mots-clés : statistiques – enquêtes – sondages – élections
[1] En anglais « straw polls ». Selon Wikipedia, ce terme ferait référence à une brindille de paille lancée en l’air pour voir de quelle direction le vent souffle …
[2] Le mot « échantillon » est pris dans ce texte dans son sens courant, « fraction d’une population destinée à être étudiée » (Petit Robert), quel que soit le procédé utilisé pour désigner cette fraction.
[3] https://www.commission-des-sondages.fr/
[4] Autrement dit, pour chaque intention de vote 1936 (Roosevelt, Landon, etc.) on dispose de la répartition des pseudo-bulletins qui mentionnaient cette intention de vote d’après le souvenir de vote 1932 (Démocrate, Républicain, etc.) qui y figurait.
[5] Plus précisément : la victoire « en nombre de grands électeurs ». On sait que l’élection présidentielle américaine est indirecte : les électeurs élisent dans chaque Etat des « grands électeurs », et ce sont ceux-ci qui élisent le Président. Il est arrivé à cinq reprises (notamment en 2000 et en 2016) qu’un candidat gagne « en grands électeurs » alors qu’il a recueilli moins de voix que son concurrent au niveau fédéral. La repondération des votes de paille 1936 renverse le résultat « en nombre de grands électeurs », pas le résultat « en nombre de voix ».
[6] Dans le cas le plus simple, la marge d’erreur d’échantillonnage est proportionnelle à la racine carrée de l’inverse de la taille de l’échantillon. Pour la diminuer de moitié, il faut prendre un échantillon quatre fois plus important.
[7] Cette marge signifie que l’intervalle indiqué a 95 % de chances de recouvrir la vraie valeur. Il reste encore 5 % des cas (un sondage de ce type sur vingt) pour que la valeur que l’on cherche à estimer soit en dehors de cet intervalle.


Commentaires récents