Investissements obligataires et profils de passif
La gestion des régimes de retraites revient à résoudre un problème assez standard: assurer au mieux le règlement de promesses de retraites dans la durée.
Au niveau mondial, les investissements obligataires de l’ensemble (OCDE) des régimes de retraites représentent approximativement 50 % du total des investissements de type obligataire réalisés par les investisseurs “institutionnels” (le secteur de l’assurance représente 40 % et celui des fonds souverains 10 % (OECD, PwC Research Center, 2016)).
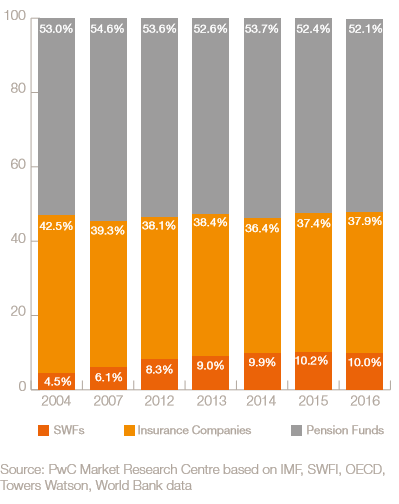
Graphique 1 : Importance relative des fonds de pensions dans les investissements des investisseurs institutionnels
En additionnant les volumes d’obligations dans les portefeuilles d’entreprises d’assurance, environ 45 % du total du marché obligataire institutionnel est ainsi détenu par des acteurs dont l’horizon d’investissement n’a cessé de s’allonger, en raison notamment de l’augmentation de la durée de vie.
Pour une cohorte d’individus nés la même année, le profil du passif d’un régime de retraite individuel décline selon une pente négative comme l’illustre le graphique 2.
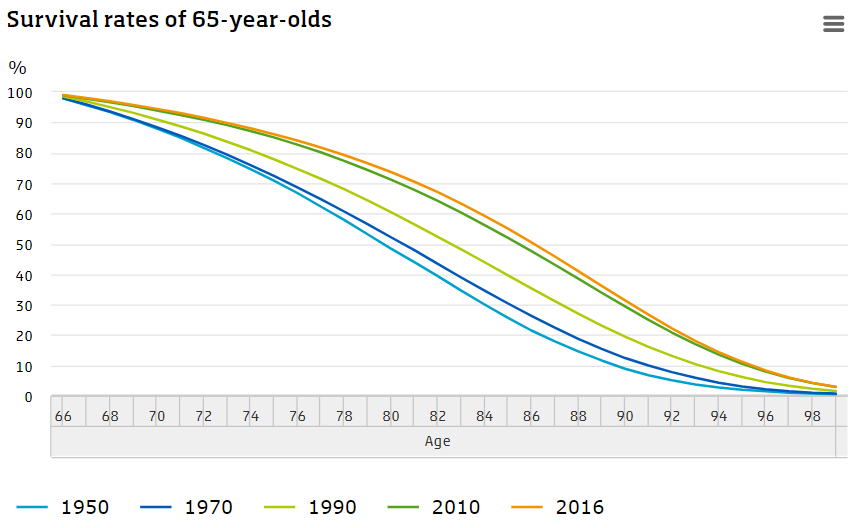
Graphique 2 : Evolution du taux de survie de cohortes âgées de 65 ans (source CBS, Statistics Netherlands)
Le profil du passif d’un fonds de pension à prestations définies, à un moment donné, est un peu différent. Pour autant, l’écoulement des flux sur les échéances longues (au-delà de 30 ans) suit également un profil dont la pente est exponentiellement négative comme illustré par le graphique 3 (Source : LGIM, Pooled Liability Driven Investments Solutions).
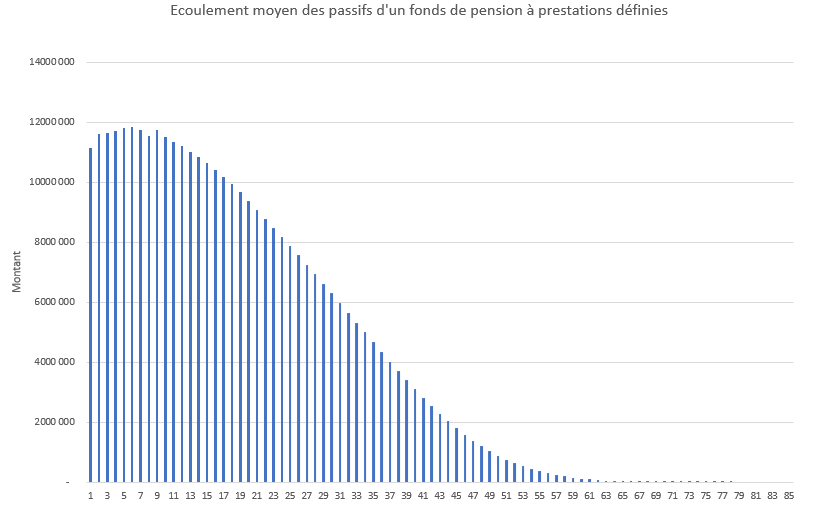
Graphique 3 : Ecoulement moyen des passifs d’un fonds de pension à prestations définies.
Ce profil de flux ne correspond pas – naturellement – à la dynamique des flux de dividendes, coupons et autres paiements issus d’un portefeuille classique constitué d’actions et d’obligations. Par ailleurs, les échéances des emprunts classiques sont inférieures à celles des engagements lointains d’un fonds de pension. Le facteur de longévité accroît encore cet effet.
Autrement dit, les marchés obligataires classiques n’offrent pas de solutions “naturelles” à l’exposition que recherche une part significative des investisseurs institutionnels lors de la gestion de leur passif.
Les obligations Evergreens
Les obligations Evergreens ont été inventées il y a une quinzaine d’années. Elles permettent d’optimiser – simplement – l’adossement des flux de revenus qui en sont issus, à l’écoulement des flux de paiements décroissants, tels que ceux requis par les engagements spécifiques de la plupart des régimes de retraites. Mais ces obligations n’existent – encore – qu’en théorie.
La solution proposée ici consiste à définir un contrat obligataire dont les caractéristiques seraient d’emblée similaires au profil “naturel” des flux issus de l’écoulement des passifs, à savoir :
- Des flux financiers qui déclinent au cours du temps (décroissance exponentielle)
- Des échéances longues
- Susceptible de faire l’objet d’un contrat à terme
- Que l’on puisse démembrer
- Qui soit fongible au sein d’une “souche” homogène et liquide, permettant d’assurer la disponibilité d’obligations en tous points similaires, quelles que soient leurs dates d’émission.
Ce contrat a été imaginé en 2005 par Chris Golden et Con Keating. Il s’agit d’un emprunt obligataire qui s’amortit de façon constante à chaque période, ne payant aucun coupon et sans échéance (perpétuel).
Exemple :
- le détenteur de € 10,000,000 d’Evergreens avec un amortissement annuel de 10 % recevra € 1,000,000 la première année, ce qui laisse un solde nominal à rembourser de € 9,000,000 ;
- à la fin de la deuxième année, le détenteur d’Evergreens recevra € 900,000, ce qui laisse un solde à rembourser de € 8,100,000 ;
- à l’issue de la troisième année, le détenteur d’Evergreens recevra € 810,000, ce qui laisse un solde à rembourser de € 7,290,000 ;
- ce processus d’amortissement exponentiel infini (en théorie) génère une infinité d’obligations à coupon zéro, comme illustré dans le graphique

Graphique 4 : Flux annuel d’une obligation Evergreens avec un taux d’amortissement de 10 % par an
Quelques caractéristiques remarquables d’une obligation Evergreens:
- En pratique, ces obligations contiennent toujours une clause conditionnelle d’échéance. Pour autant, une obligation d’une durée de vie moyenne de 20 ans attendra 300 ans la date du dernier paiement.
- De même, une obligation d’un même montant et d’une durée de vie moyenne de 2 ans permet de régler des flux au-delà de 25 ans.
- Une obligation zéro coupon conventionnelle remboursable dans 50 ans est assortie d’une échéance contractuelle de 50 ans et d’une durée de vie moyenne de 50 ans.
- Une obligation Evergreen d’une durée de vie moyenne de 20 ans effectuera un règlement représentant encore 4 % du nominal à la fin de la 50ème année (et davantage avant cette date).
- De même, la duration de cette obligation (amortissement annuel de 4 %) est de 11,11 ans.
- L’autosimilarité des flux au cours du temps se traduit par une durée de vie moyenne très stable.
- De même, les mesures de duration et de convexité de l’obligation Evergreen sont extrêmement stables dans le temps.
- La rémanence des mesures de sensibilité permet de mettre en place des souches uniques d’émission, caractérisées par le seul taux d’amortissement.
- Un fonds de pension dispose ainsi d’un accès permanent à une même souche d’obligations Evergreens. Les émissions d’emprunts issues d’une souche deviennent entièrement fongibles.
- La sensibilité de l’obligation Evergreens à l’ensemble de la courbe des taux est stable :
- La distribution des flux au cours du temps est régulière (à l’inverse d’un emprunt obligataire).
- La contribution à la mesure de la duration (et de la convexité) est régulière en l’absence de flux dominant (Graphique 5).
- L’obligation Evergreens est relativement plus convexe que n’importe quelle obligation classique à l’exception des annuités.
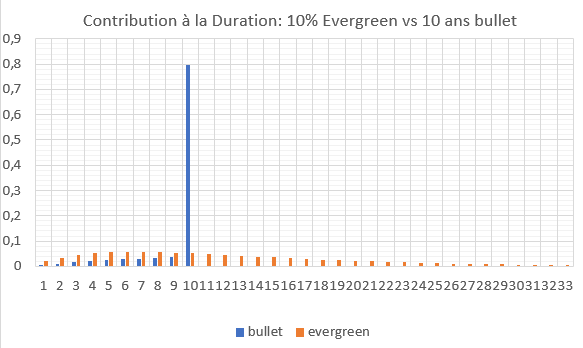
Graphique 5 : Contribution à la duration
De l’intérêt de combiner des obligations Evergreens
Le graphique 6 illustre l’adossement d’un portefeuille constitué de deux souches distinctes d’Evergreens à un passif de prestations définies (exemple réel). On observe l’évolution de l’impasse et de l’excédent de trésorerie en fonction de l’âge de la cohorte. Cet excédent de trésorerie sur l’horizon lointain permet de gérer l’augmentation de la longévité.
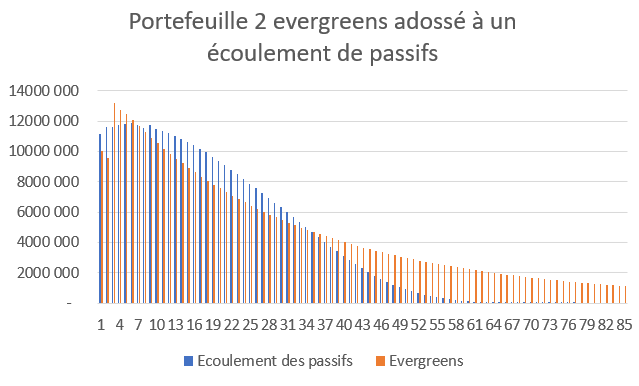
Graphique 6 : Profils de flux d’un portefeuille constitué de 2 Evergreens
En terme de gestion actif/passif, cette approche permet de satisfaire les conditions d’immunisation de façon plus simple et plus stable que celles résultant de l’adossement des mesures de duration et convexité issues de l’utilisation d’obligations classiques.
Un portefeuille d’obligations Evergreens permet de contribuer à résoudre le problème de l’accroissement de longévité. Imaginons un portefeuille constitué – à parts égales – d’obligations Evergreens “2 ans” et d’obligations Evergreens “50 ans”. La durée de vie moyenne de ce portefeuille est de 26 ans. Dans un an, 50 % de l’Evergreen “2 ans” et 2 % de l’Evergreen “50 ans”, sont remboursés ; la durée de vie moyenne dans un an a ainsi augmenté à 33,784 années. Cet exemple illustre la dynamique de la durée de vie moyenne d’un portefeuille d’Evergreens, utile pour gérer l’accroissement de longévité des passifs (graphique 7).
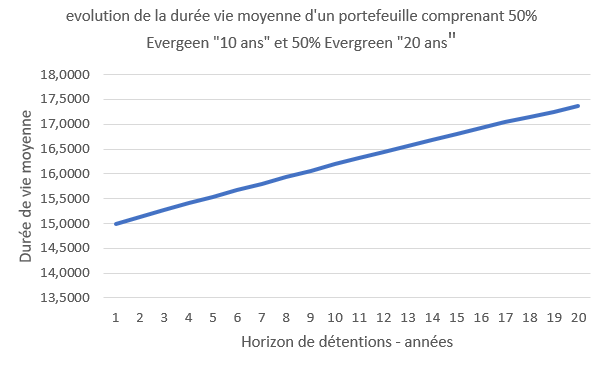
Graphique 7 : Obligations Evergreens et accroissement de la longévité des passifs
De la liquidité des Evergreens et de leur capacité à intégrer le marché secondaire classique
Sur les marchés primaires clasiques, les souches d’Evergreens peuvent être activées par l’émetteur selon ses besoins et les préférences des investisseurs en terme de taux d’amortissement.
La liquidité des emprunts Evergreens serait appelée à dominer celle des souches d’emprunts classiques en raison notamment de :
- l’augmentation régulière de la taille de chaque souche en fonction de son utilisation,
- l’absence du facteur de vieillissement de l’emprunt Evergreen (puisqu’il est perpétuel),
- leur statut permanent d’emprunt de référence (à l’inverse des grands emprunts d’Etat classiques dont le vieillissement entraine la perte de leur statut de référence),
- l’intérêt de l’investisseur sur l’émission en cours, facteur essentiel dans la manifestation du prix de marché.
De plus, des schémas de titrisation d’obligations classiques permettent d’envisager leurs « recyclages » sous la forme d’Evergreens par le biais de véhicules de titrisation permanents. Ces souches sont ensuite alimentées par les émissions classiques provenant du marché secondaire. Des tests effectués sur divers indices obligataires à différentes périodes semblent confirmer cette idée et sa stabilité au cours du temps.
Les enjeux d’une telle innovation
Le fonctionnement des marchés obligataires repose sur une contractualisation standardisée et des principes de valorisation. Ces règles assurent une certaine homogénéité aux contrats, la fluidité des transactions et, partant, l’adoption éventuelle de l’innovation par les acteurs du marché.
Parmi ces innovations, on peut citer le démembrement des obligations souveraines aux Etats-Unis et dans plusieurs pays européens dès le début des années quatre-vingt-dix.
Mais l’exemple le plus pertinent est le développement des titres adossés à des créances hypothécaires (Mortgage Backed Securities) aux Etats-Unis. Cette innovation trouve son origine dans le New Deal, un ensemble de mesures prises aux Etats-Unis, à la suite de la crise de 1929.
Afin de relancer le secteur de la construction, le gouvernement américain apporta sa garantie au remboursement du capital et des intérêts de pools de créances hypothécaires lorsque celles-ci remplissaient certaines conditions. Cette mission fut confiée à une agence fédérale, la FHA (Federal Housing Association). Dès 1938, une nouvelle agence sera créée, Fannie Mae, dont la mission initiale sera d’assurer un marché secondaire à ces titres de créances. Dans les années 60, ce mécanisme sera étendu à d’autres agences (GNMA, Freddie Mac principalement) afin de permettre le refinancement de créances hypothécaires privées.
Cette innovation permit d’éliminer le remboursement « in fine » d’un emprunt hypothécaire, en intégrant le remboursement du capital dans les flux constants de remboursement. Ce faisant, cette innovation permettait de réduire sensiblement le risque de crédit supporté par le contribuable américain.
La taille de ce marché a crû très rapidement au point de parfois dépasser celle du marché des obligations d’Etat (pour autant, ce marché ne sera jamais vraiment liquide, en raison notamment de l’optionalité inhérente aux emprunts à taux fixes).
On retiendra que cette innovation :
- fut le résultat d’une volonté politique forte visant la relance du secteur de la construction à la suite de la crise de 1929 et ensuite de la seconde guerre mondiale,
- repose sur les marchés de capitaux (80 % du financement de l’économie américaine) et non sur le secteur bancaire (70 % du financement de l’économie européenne),
- bénéficie de la garantie, implicite ou explicite selon les agences, des pouvoirs publics et, partant, d’une bienveillance (coupable ?) du régulateur,
- permet d’adosser plus naturellement les flux de revenus des ménages aux flux de leurs charges financières.
Mutatis mutandis, on peut résumer ainsi la liste des conditions qui seraient nécessaires (mais pas suffisantes) à l’adoption des obligations Evergreens :
- la reconnaissance d’un problème de financement long (besoin de financement des régimes de retraites, infrastructures, etc..)
- la nécessité d’une initiative publique forte (des emprunteurs souverains prennent l’initiative d’émettre des obligations Evergreens)
- le régulateur établit un cadre réglementaire et prudentiel favorable à ce type d’investissement.
Conclusions
Les obligations Evergreens répondent de façon optimale aux besoins de financement caractérisés par une décroissance des flux (de passif) sur des horizons longs tels que :
- l’espérance de vie d’une population ou d’une cohorte spécifique
- le règlement des intérêts d’un emprunt hypothécaire
- le financement de projets de long terme (de type infrastructure)
- le financement du passif de régimes de retraites par capitalisation, individuels ou semi-collectifs ou encore des portefeuilles d’assurance-vie
Cette capacité de réplication, combinée avec la stabilité des mesures de sensibilité aux taux d’intérêt, permet une maîtrise optimale du risque de taux.
La liquidité des emprunts Evergreens dominerait rapidement celle des souches d’emprunts classiques.
De plus, des schémas de titrisation d’obligations classiques permettraient d’envisager leur « recyclage » sous la forme d’Evergreens.
Le développement des obligations Evergreens repose sur l’examen plus approfondi des conditions de leur mise en œuvre sur le plan contractuel, réglementaire et prudentiel.
Leur adoption par un émetteur souverain (ou multilatéral) et la mise en place d’un partenariat avec l’une ou l’autre des associations professionnelles permettraient de faire progresser cette idée.
Mots-clés : Obligations – gestion actif/passif – perpétuité
Annexe 1 : le prix de marché d’un Evergreen
Le prix de marché est déterminé par la référence instantanée au rendement spot observé sur la courbe des taux pour une échéance correspondante. Pour les raisons indiquées plus tôt (conditions de liquidité, agencement des flux optimisé), le prix d’émission serait vraisemblablement plus élevé (et donc le rendement inférieur aux taux spot de référence).
De plus, l’emprunt Evergreen – contrairement à son homologue remboursable in fine – bénéficie d’une meilleure qualité de crédit en raison des faibles montants dus sur les durées longues, ce qui est susceptible d’améliorer les conditions de son émission. Les institutions financières spécialisées dans le financement d’infrastructures seraient, à cet égard, les émetteurs privilégiés de ce type d’instrument.
Annexe 2 : résumé du développement mathématique :
est le taux d’amortissement de l’obligation Evergreen
est la durée de vie moyenne de l’obligation
est le prix d’une l’obligation zéro coupon d’échéance n
est la valeur d’un paiement en période n
est le prix de l’obligation Evergreen
est le taux de interne de rentabilité (yield)
est la Duration modifiée de l’obligation Evergreen
est la Duration de Macaulay de l’obligation Evergreen
est la Convexité de l’obligation Evergreen
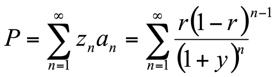
Soit
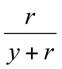
Et
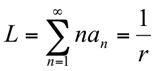
Et
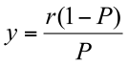
Et
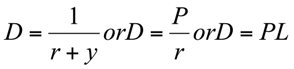
Et
![]()
Et
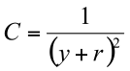
- Obligation Evergreens :variations sur un thème - 23 septembre 2019

Commentaires récents