1. Introduction
L’estimation du risque biométrique et plus particulièrement la modélisation de la longévité remonte aux origines de la science actuarielle au milieu du 17ème siècle. A cette époque, les Etats et les villes ont souvent recours à l’emprunt en émettant des rentes viagères à leurs citoyens.
Une des premières études sur ce sujet fut réalisée par Jan de Witt, premier ministre des Etats de Hollande. Jan de Witt démontra en 1671 comment calculer la valeur des rentes en utilisant un taux d’intérêt constant et une table de mortalité hypothétique introduisant ainsi les probabilités sur la durée de la vie humaine.
Si la notion d’espérance de vie est apparue pour la première fois en 1746 dans le travail d’Antoine Deparcieux, « Essai sur les probabilités de la durée de vie humaine »[1], des calculs réalisés par Lodewijk Huygens[2] apparaissent dans sa correspondance avec son frère Christiaan en 1669. Il estime que son frère vivra jusqu’à l’âge de 56 ans et demi, et lui jusqu’à l’âge de 55 ans. Pour l’anecdote, Christiaan et Lodewijk Huygens décédèrent à 66 et 68 ans.
L’importance de construire une table de mortalité basée sur un recensement plutôt que de manière hypothétique a été rapidement reconnue. Les premières observations furent obtenues à partir des registres paroissiaux et permirent de connaître la répartition de la population selon l’âge.
En 1808, le gouvernement britannique, pressé par la guerre avec Napoléon Ier et l’inflation, décida d’émettre des rentes pour tenter de réduire la dette nationale. Ces rentes étaient évaluées en utilisant les taux d’une table de mortalité conçue en 1780 à partir de registres paroissiaux de Northampton. Les tables de Northampton n’étaient pas très conservatrices et ne tenaient pas compte d’une sélection défavorable parmi les détenteurs de rentes viagères, i.e. la tendance pour les acheteurs de rentes viagères à vivre plus longtemps que la population générale. Cette sous-estimation de la mortalité des rentiers a fait perdre plusieurs millions de livres au gouvernement britannique[3].
Par la suite, la présence d’une tendance à la baisse de la mortalité à partir du début du 20ème siècle a incité les émetteurs de rentes à inclure les améliorations futures des taux de mortalité afin de se prémunir des pertes futures. Les premières tables prenant en compte ce phénomène ont été celles produites au Royaume-Uni sur la base de données de compagnies d’assurance couvrant la période 1900-1920.
De nos jours, les hypothèses de mortalité d’un portefeuille de rentiers sont construites en deux étapes. Il s’agit d’une part de mesurer la mortalité des rentiers, afin d’en déduire le niveau de mortalité aujourd’hui. D’autre part, des projections de la mortalité dans le futur lui sont appliquées de façon à anticiper les tendances à la baisse de mortalité. C’est cette dernière composante du risque de longévité qui sera développée dans la suite de cet article.
2. Dynamique de la mortalité dans le temps et grandes phases de changements socio-économiques
Considérons une personne d’âge et désignons par
la variable aléatoire représentant sa durée de vie restante à l’année
. En notation actuarielle, la probabilité
qu’un individu âgé
durant l’année calendaire
atteigne l’âge
et
la probabilité qu’un individu âgé
durant l’année calendaire
décède avant d’atteindre l’âge
sont généralement employées.
La tendance des probabilités annuelles de décès observées pour la population masculine du Royaume-Uni pour les âges 20, 40, 60 et 80 ans est présentée Figure 1. Les données proviennent de Human Mortality Database (2017)[4]. Les courbes sont soumises à des chocs de période correspondant à des guerres, des épidémies, canicules, etc. Il est évident que des changements importants de la mortalité se sont produits au cours du 20ème siècle, comme en témoignent les tendances à la baisse et les variations de forme.
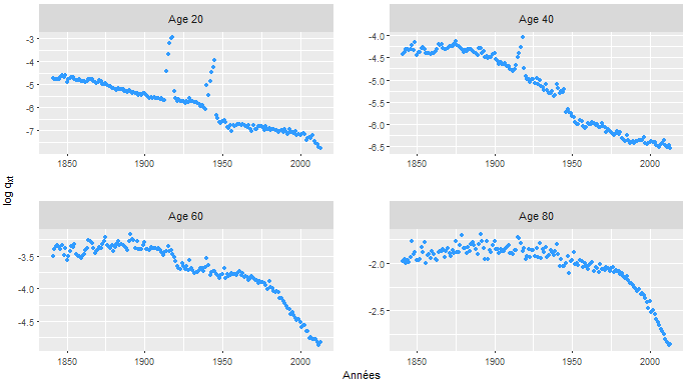
Figure 1 : Taux de mortalité, population masculine, Royaume-Uni, échelle logarithmique, pour les âges 20, 40, 60 et 80 ans.
Au fil du temps la mortalité a diminué pour la population masculine à tous les âges sans interruption mais à des vitesses différentes. À l’âge de 20 ans, une réduction rapide de la mortalité a eu lieu après un pic au début des années 1940 dû à la Seconde Guerre mondiale. Cependant, depuis les années 1950, seules de modestes améliorations se sont produites. Ceci est typique pour les âges autour de la bosse des accidents . La mortalité masculine des jeunes adultes n’a pas vraiment diminué depuis les années 1970. Entre 1980 et le milieu des années 1990, l’apparition du sida a eu une influence négative sur la réduction de la mortalité. À l’âge de 40 ans, une diminution similaire est présente après la Seconde Guerre mondiale, suivie d’une réduction beaucoup plus lente de la mortalité après 1960. La diminution après 1970 est plus marquée qu’à 20 ans. À l’âge de 60 ans, les taux de mortalité ont diminué rapidement après 1970, alors que la baisse au cours des années 1850-1970 était plus modérée. À l’âge de 80 ans, cette diminution apparait après 1990.
La Figure 2 illustre le lien étroit entre développements socio-économiques et l’évolution de la mortalité à 80 ans de la population masculine au Royaume-Uni entre 1840 et 2009. La Figure 3 présente l’évolution des améliorations de mortalité pour la population masculine de 75-85 ans au Royaume-Uni sur la même période. Les améliorations de mortalité, notées représentent le pourcentage de baisse de la mortalité à l’âge
entre l’année calendaire
et
,
.
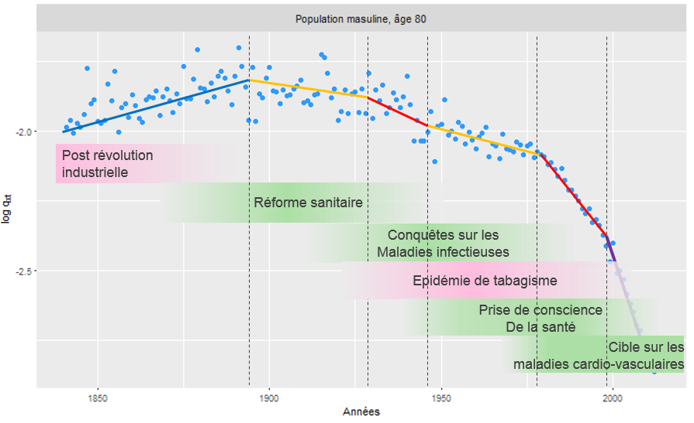
Figure 2 : Taux de mortalité observés à 80 ans, population masculine, Royaume-Uni sur la période 1841 – 2013 et grands développements socio-économiques
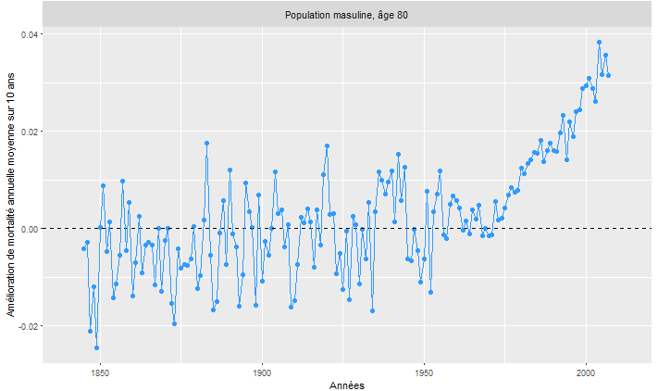
Figure 3 : Amélioration de mortalité annuelle moyenne sur 10 ans, population masculine, Royaume-Uni sur la période 1841-2012
Les grandes phases de changements socio-économiques peuvent être identifiées Figure 2. Ce sont nécessairement des interprétations simplistes des avancées sociales et médicales complexes, mais elles indiquent que les dynamiques de la mortalité changent au fil du temps.
La période qui a suivi la révolution industrielle au Royaume-Uni, 1840-1890, est marquée par une migration massive de plus de la moitié de la population des zones rurales vers les zones urbaines avec de mauvaises infrastructures et des conditions sanitaires insalubres. Les maladies infectieuses et notamment le choléra sont une menace constante. Les taux de mortalité augmentent au cours de cette période impliquant une détérioration de la mortalité et une fluctuation importante due aux épidémies, Figure 3.
Les conditions insalubres qui prévalaient dans les villes ont été reconnues comme des problèmes de santé publique. Une réforme sanitaire fut mise en place, dans les années 1890-1930, marquée par des investissements importants dans les infrastructures urbaines avec des systèmes d’assainissement et de fourniture en eau propre. Les épidémies et notamment la pandémie de grippe espagnole, causent des chocs de mortalité, mais l’évolution de la mortalité est généralement positive.
La science médicale a identifié les causes des maladies infectieuses comme la tuberculose et les traitements deviennent disponibles. C’est le début de la conquête sur les maladies infectieuses pendant la période 1920-1960. La pénicilline a d’abord été identifiée en 1928 et produite en masse après 1945. Les antibiotiques sont devenus disponibles dans le commerce après les années 1930.
Les taux de mortalité liés à la tuberculose, un tueur majeur au début du 20ème siècle, ont été divisés par deux en 1930 et ont diminué de moitié en 1950 grâce à l’éducation sanitaire et aux traitements contre la streptomycine. La réduction de la mortalité est particulièrement marquée chez les moins de 45 ans. Par ailleurs, les améliorations de la mortalité pour les hommes entre 75 et 80 ans sont également élevées, atteignant près de 2% vers la fin de cette période.
Avec la création du National Health Care Service en 1947, les soins de santé sont devenus universellement disponibles. Mais cette avancée sociale coïncide avec l’austérité de l’après-guerre. Durant la période 1940-1970, le tabagisme n’est pas reconnu comme un danger pour la santé et devient une habitude populaire. La diminution de la mortalité est faible et on observe des périodes de détérioration.
Les premières études reliant le tabagisme à la mortalité sont réalisées en 1956, cependant la prise de conscience publique n’est survenue que deux décennies plus tard en 1970. Celle-ci inclut le régime alimentaire, l’exercice physique et la prévention des accidents. Les taux de mortalité déclinent rapidement. Les oscillations des améliorations de mortalité ont cessé.
Depuis les années 90, le dépistage systématique de l’hypertension artérielle est introduit avec la prescription de médicaments antihypertenseurs à grande échelle impactant plus de 20% de la population âgée au Royaume-Uni. Les progrès médicaux en matière de chirurgie cardiaque améliorent considérablement les taux de survie post AVC. Les améliorations de mortalité augmentent à leur niveau record de 3%.
La Figure 4 illustre la dynamique de la mortalité représentée par les améliorations de la mortalité observée pour la tranche d’âge 20-100 ans sur la période 1960-2012 pour la population masculine du Royaume-Uni. L’échelle de couleur montre l’intensité des améliorations de mortalité (vers le rouge pour des améliorations élevées). Les améliorations de mortalité ne varient pas uniformément selon l’âge et l’année calendaire.
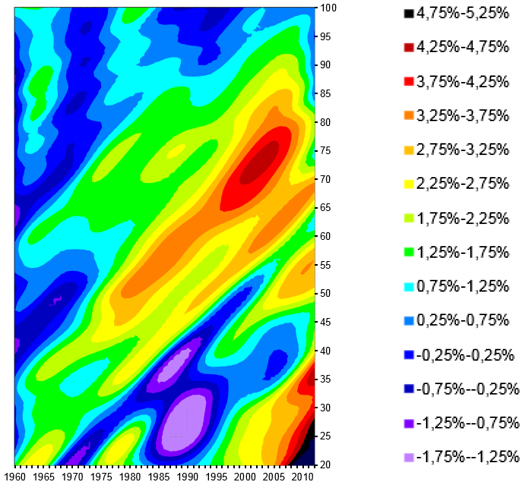
Figure 4 : Amélioration de la mortalité lissée, population masculine, Royaume-Uni, tranche d’âge : 20-100 pour la période 1841-2012
L’avantage de cette figure est qu’elle facilite la visualisation des changements dans les améliorations de mortalité par année calendaire et par âge ainsi que par génération (année de naissance).
Des structures de couleurs verticales indiquent des effets de période, alors que les effets dits générationnels ou de cohorte apparaissent diagonalement de gauche à droite. Par exemple, un homme âgé de 45 ans en 1980 est soumis à un effet de cohorte qui persiste à l’âge 46 ans en 1981, 47 ans en 1982, etc… illustré par la diagonale orange et jaune commençant au centre de la Figure 4.
Les effets de périodes indiquent un changement observé dans les améliorations de mortalité affectant tous (ou la plupart) les âges durant certaines périodes ou années calendaires. Ces effets résument les facteurs contemporains comme l’état de santé générale de la population, la disponibilité et l’accès aux services de santé ou les conditions météorologiques critiques.
Les effets de cohortes montrent que différents groupes (ou cohortes) d’individus nés à la même période peuvent avoir tendance à subir des améliorations de mortalité identiques. Les raisons de ces effets de cohorte ne sont pas encore bien comprises. Un certain nombre de facteurs explicatifs ont été suggérés dans la littérature[5]. L’introduction d’un système universel de sécurité sociale en 1948 (suite au rapport Beveridge de 1942), l’introduction de l’enseignement secondaire gratuit pour tous en 1944 et la création du Service national de santé en 1947 signifiaient que les conditions sociales pour les enfants grandissant dans les années 1950 étaient très différentes de celles vécues par les générations précédentes. Il existe aussi de fortes tendances générationnelles dans la mortalité dues à des maladies liées au tabac comme le cancer du poumon et les maladies cardiaques. Au Royaume-Uni et ailleurs, différentes générations ont eu différents comportements liés au tabagisme. L’impact du tabac sur la santé a été identifié à la fin des années 1950 et les comportements ont commencé à changer 20 ans plus tard. Il y a un contraste marqué avec la génération d’après-guerre (née entre 1945 et 1950) illustrée par la diagonale bleue qui a atteint l’âge adulte avant la prise de conscience de la dangerosité du tabac.
3. Projection de la mortalité
La prise en compte des tendances futures de la mortalité (et éventuellement de l’incertitude présente) est nécessaire dans un certain nombre de calculs et d’applications actuariels. En particulier, ceux qui concernent les pensions, les rentes viagères et autres avantages sociaux prévus, par exemple, dans les cas de la dépendance et de maladies de longue durée. Ces calculs se basent sur les probabilités de survie qui s’étendent sur un horizon à long terme.
Pour éviter de sous-estimer ses passifs, la compagnie d’assurance (ou le régime de retraite) doit avoir une prévision appropriée de la mortalité future, qui doit tenir compte des caractéristiques les plus importantes de la dynamique de la mortalité passée.
Ces tendances de mortalité peuvent être prises en compte en examinant le comportement, dans le temps, de la mortalité en fonction de l’âge et de l’année de naissance. Les exemples décrits à la section 2 illustrent clairement ce fait. La mortalité doit être modélisée sous la forme d’une entité dynamique, tant d’un point de vue formel que pratique, pour la projection et la prévision de la mortalité future.
La première étude sur la projection de la mortalité future fut probablement l’œuvre de l’astronome suédois Hugo Gyldén en 1875[6]. Gyldén ajusta une droite aux taux de mortalité de la population suédoise sur la période 1750-1870 et suggéra que cette droite pourrait être considérée comme une prévision probable des taux de mortalité futurs. La dernière année d’observation donnait un taux de décès de 19,8‰ en 1870. Gyldén donna le chiffre de 17,7‰ comme estimation du taux de mortalité pour l’année 1900. En réalité, le taux de mortalité observé fut de 16,8 ‰. La méthode utilisée par Gyldén est évidemment très primitive et sa proposition de projection ne concerne qu’un seul indice pour tous les âges.
En 1912, une table de mortalité pour les rentes a été construite par un autre astronome et mathématicien suédois Andres Lindstedt, qui utilisa des données de la population suédoise jusqu’en 1907. Pour chaque âge, Lindstedt extrapola les probabilités annuelles de décès, adoptant ainsi une approche horizontale. Ce travail constitue probablement la projection la plus ancienne en fonction de l’âge. La table extrapolée fut largement utilisée en Suède et correspondait assez bien à l’expérience observée pendant la période 1911-1915. Dans l’explication de sa méthode, Lindstedt souligna la nécessité de baser les prévisions sur une extrapolation des changements de la mortalité passée.
Parmi les modèles de prévision proposés, une méthode de projection selon l’âge a constitué une des propositions les plus influentes de ces dernières décennies. Alors que les modèles de projections traditionnelles fournissent une estimation ponctuelle des taux de mortalité futurs, la méthode proposée, puis prolongée par Lawrence Carter et Ronald Lee permet explicitement des fluctuations aléatoires de la mortalité future[7]. La méthode consiste à scinder l’évolution de la mortalité en trois composantes, l’une propre à l’âge modélisant le comportement moyen de la mortalité au cours du temps, une autre décrivant l’écart de la mortalité par rapport au comportement moyen et une tendancielle capturant l’évolution de la mortalité, et ensuite à extrapoler cette dernière dans le futur. L’avantage de cette méthode est de réduire le problème de la projection de la mortalité à l’étude d’une série chronologique. De nombreuses généralisations et améliorations ont été proposées, qui suivent et s’appuient sur les idées fondamentales de la méthodologie de Lee et Carter[8].
Enfin, il convient de rappeler que les modèles présentés brièvement ici n’intègrent pas les hypothèses sur les progrès de la science médicale ou les changements environnementaux. Aucune information autre que les données passées n’est prise en compte. L’hypothèse sous-jacente est que toute l’information sur l’avenir est contenue dans les taux de mortalité observés dans le passé. En d’autres termes, ces approches sont incapables de prévoir des améliorations soudaines de la mortalité grâce à des innovations en matière de santé publique par exemple. De même, les détériorations futures causées par les épidémies ou la dégradation de l’environnement ne peuvent être prises en compte. Les méthodes dites de « table optimale » offrent une approche alternative pour dériver les prévisions de mortalité en intégrant une procédure d’interpolation entre les données passées et une mortalité à long terme déterminée au préalable.
[1] Voir Charpentier, A. (2007). Ajuster les tables de mortalité, le rôle des actuaires. Risques, 72, pp 127-130.
[2] Voir Véron, J. et Rohrbasser, J.-M. (2000). Lodewijk et Christiaan Huygens: La distinction entre vie moyenne et vie probable. Mathématiques et Sciences Humaines, 38(149), pp 7-21.
[3] Hacking, I. (1975). The emergence of probability: A philosophical study of early ideas about probability, induction and statistical inference. Cambridge University Press.
[4] Human Mortality Database (2017). University of California, Berkeley (USA), and Max Planck Institute for Demographic Research (Germany). Disponible à www.mortality.org ou www.humanmortality.de. Ce projet international fournit des données détaillées sur la mortalité et la démographie à des fins de recherche.
[5] Willets, R. C. (2004). The cohort effect: insights and explanations. British Actuarial Journal, 10, pp 833-877.
[6] Voir Cramér, H. et Wold, H. (1935). Mortality variations in Sweden: a study in graduation and forecasting. Scandinavian Actuarial Journal, pp 161-241.
[7] Voir Lee, R. D. et Carter, L. R. (1992). Modelling and forecasting U.S. mortality. Journal of the American Statistical Association, 87(14), pp 659-675.
[8] En particulier : Renshaw, A. E. et Haberman, S. (2006). A cohort-based extension to the Lee–Carter model for mortality reduction factors. Insurance: Mathematics & Economics, 38(3), pp 556-570 ; Brouhns, N., Denuit, M., et Vermunt, J. K. (2002). A Poisson log bilinear approach to the construction of projected lifetables. Insurance: Mathematics & Economics, 31(3), pp 373-393 ; et les travaux de Cairns, A. J. G., Blake, D., et Dowd, K. (2006). A two-factor model for stochastic mortality with parameter uncertainty: theory and calibration. The Journal of Risk and Insurance, 73(4), pp 687-718 ; et Cairns, A. J. G., Blake, D., Dowd, K., Coughlan, G. D., Epstein, D., et Khalaf-Allah, M. (2011). Mortality density forecasts: An analysis of six stochastic mortality models », Insurance: Mathematics and Economics, 48(3): pp 355-367.
- Dynamique de la mortalité : Historique et techniques actuarielles - 8 novembre 2017

Commentaires récents