Abstract : In sporting event, the installation of a game handicap rule is an often delicate problem. Certain sports as tennis or golf solve the question by defining a nomenclature of classification based on this notion of handicap. Therefore, numerous club of table tennis organize tournament based on various game handicap formulas. We offer a probabilistic approach allowing to define, a rational, fair and simple rule of game handicap.

  1. INTRODUCTION

La mise au point d’une règle de handicap est une étape indispensable dans tous les sports. En effet, permettre à deux joueurs, de classements différents, de se mesurer en rééquilibrant les chances de victoire de l’un et de l’autre est une nécessité à l’entrainement comme pour certaines compétitions. Pour certains sports comme le tennis ou le golf, c’est cette notion de handicap qui est à l’origine des classements eux-mêmes. Au tennis de table, la méthode de classement n’est apparemment construite sur aucune notion de handicap de jeu. Pour autant, dès qu’une procédure de classement existe, il est possible d’en déduire une distance probabiliste entre deux classés et de compenser cet écart de probabilité de victoire par une règle de handicap de jeu. Nous proposons une méthode d’estimation des distances probabilistes entre les classements au tennis de table. Ces distances permettent alors de construire une règle de handicap qui a été expérimentée.

  1. PROBABILITE DE GAGNER LA PARTIE

Au tennis de table, chaque partie en compétition officielle participe au calcul du classement. En fonction de l’issue de la partie et de l’écart de points de classement entre les 2 joueurs, le vainqueur augmente son nombre de points et le perdant le diminue selon un tableau définit par la FFTT (tableau 1).

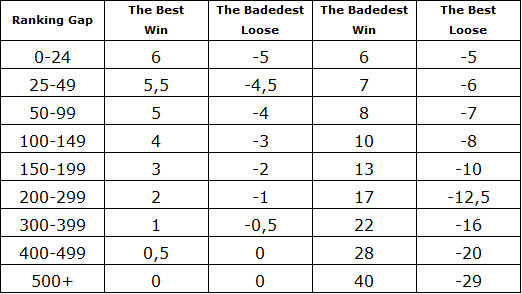
Tableau 1 (source FFTT-2013)

En théorie des jeux (Binmore 1999), on estime qu’un jeu est équilibré si l’espérance de gain est nulle pour les deux joueurs («jeu à somme nulle»). Plus précisément, lorsque deux joueurs A et B se rencontrent et que la probabilité que A gagne la partie est notée P_{A}(avec P_{A} \leq \frac{1}{{2}}), alors le jeu est à somme nulle si les points de classement échangés ( K_{A} et K_{B}) sont tels que :

Donc :

De ce principe, on est en mesure de calculer pour tout K_{A}  et K_{B} du tableau 1 et donc pour tout écart de classement entre deux joueurs, la probabilité que le mieux classé sorte vainqueur (P_{A} ).

Normalement (pour un jeu à somme nulle), pour un même écart de classement, les probabilités de victoires normales (the best win) et de défaites anormales (the best loose) devraient avoir une somme égale à 1. De même pour les probabilités de victoires anormales et de défaites normales. Ce n’est pas exactement le cas. En particulier, pour un écart de points entre 0 et 24, nous devrions avoir des probabilités toutes égales à 1/2. L’attribution actuelle des points n’est donc pas exactement la solution d’un jeu à somme nulle.

Néanmoins, ces calculs produisent un encadrement de chaque probabilité. Il est alors naturel de prendre comme probabilité, le milieu de chaque intervalle comme le montre graphique 1.

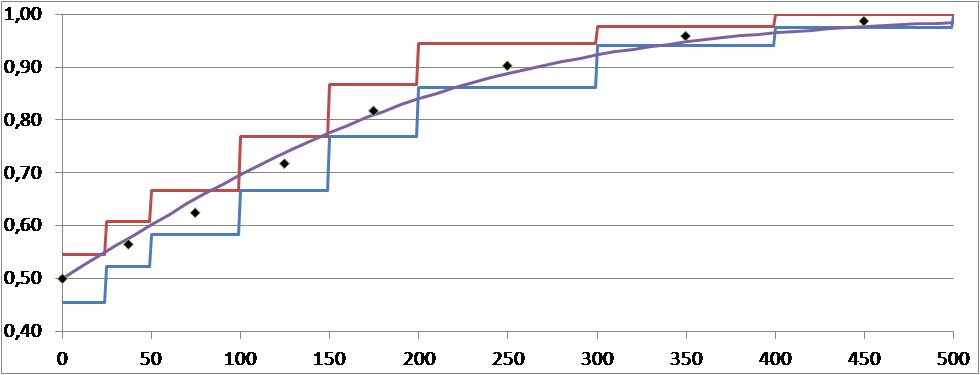
Graphique 1 : Probabilités de victoire moyennes lissées par le modèle de Bradley-Terry (1952)

  1. PROBABILITE DE GAGNER LE POINT

Au tennis de table, une partie « classique » se joue au meilleur des 5 manches de 11 points. Il est ici possible de mettre en relation la probabilité de victoire d’une partie à handicap P(p,H) en fonction de la probabilité, p, de victoire du point (voir Sarfati et al. (2000) pour le tennis sans handicap de jeu).

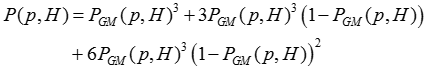
avec P_{{GM}}(p,H),  la probabilité de gagner une manche avec le handicap H :

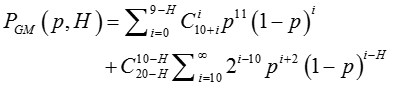
H = 1, 2, etc…, cela signifie que le joueur le moins bien classé commence chaque manche non pas à 0 mais avec 1 ou 2 …  points d’avance en fonction de sa probabilité (à priori) de victoire de la partie (sans handicap).

  1. ETAPE DE CONSTRUCTION DU HANDICAP DE JEU

(1) On estime  P(p,0) pour chaque écart de classement défini dans le tableau d’attribution des points de la FFTT (réalisé avec le modèle de Bradley-Terry). (2) Par résolution de l’équation P(p,H) pour H=0, on estime la probabilité, p, de gagner un point en fonction de la probabilité de gagner la partie sans handicap P(p,0). (3) Par résolution de l’équation P(p,H) pour H=1, 2,…, on estime la probabilité de gagner le point, p_{H}  , pour un handicap H qui conduit à une probabilité de gagner la partie P(p_{{H,}}H )=\frac{1}{2}. (4) par calcul direct de l’équation pour H=0, on estime alors la probabilité de gagner la partie sans handicap P(p_{{H,}}0 ) . (5) En mettant en correspondance P(p, 0 )  et P(p_{{H,}}0 ) , on obtient les écarts de points de classement équivalents à chaque handicap H.

  1. RESULTATS

Le graphique 2 montre que la relation entre l’écart de classement et le « juste » handicap est linéaire. On est alors en mesure de proposer un handicap de jeu très simple (voir Tableau 2).

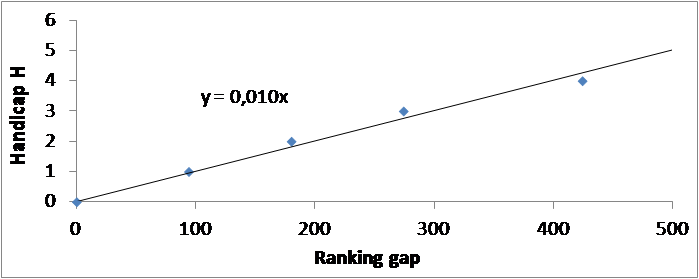
Graphique 2 : Relation entre écart de classement et handicap de jeu positif

 

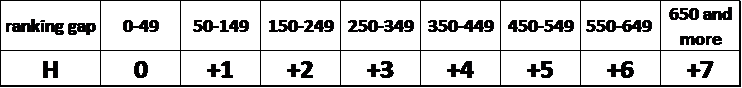
Tableau 2 : Règle théorique de Handicap positif

Par exemple, un 1300 qui rencontre un 1430 commencera chaque manche à +1. Ici il est nécessaire que ce handicap n’augmente pas indéfiniment. En effet, un handicap de +11 donnerait systématiquement la partie au joueur le moins bien classé. Nous considérons alors que +7 est le handicap maximum acceptable par les joueurs.

  1. CONCLUSION

Mettre en œuvre un principe de match par handicap ne doit pas être une opération subjective issue d’un processus d’essai-erreur. C’est une conséquence directe de la procédure de classement elle-même. Une bonne règle de handicap doit « remettre les compteurs à 0 ».

La  règle de handicap proposée est basée sur une probabilité de victoire égale pour les deux joueurs, quelques soient leurs différences de classement. On peut se poser la question de l’intérêt pour le joueur le mieux classé de participer à ce type de rencontre. En effet, la remise des « compteurs à zéro » est à « l’avantage » du joueur le plus faible.

Afin de conserver une position ascendante, plus symbolique que significative, nous proposons de conserver un très léger avantage au joueur le mieux classé. Aussi, la règle « d’avantage » de jeux que nous proposons est la suivante :

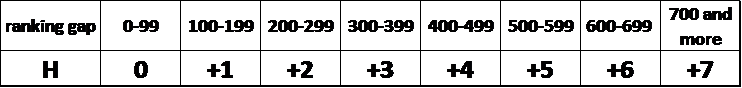
Tableau 3 : règle retenue des handicaps de jeu

Par exemple, si l’écart de classement entre les deux joueurs est de 215 points, le joueur le moins bien classé commencera chaque manche avec 2 points d’avance.

Afin d’éprouver cette proposition de règle de jeu, un tableau à handicap a été organisé dans deux tournois régionaux girondins en 2013. Le tableau était ouvert aux joueurs non licenciés, licenciés promotionnelles et licenciés traditionnelles, ces derniers classés jusqu’à 1299. Une trentaine de joueurs ont participé à chacun de ces tournois. Au total, plus de 120 rencontres ont été disputées. L’analyse statistique des résultats des rencontres porte sur les 44 rencontres qui opposaient deux joueurs avec licence traditionnelle dont le classement était strictement supérieur à 500 points et dont le handicap de jeu était strictement positif. En effet, le niveau des non licenciés ou des licenciés à 500 points est trop hétérogène pour que les rencontres comportant un joueur de ce type soient incluses dans l’analyse.

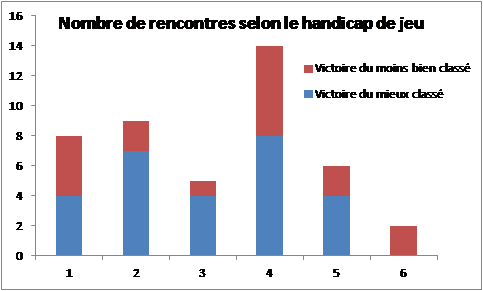
Sur les 44 rencontres, 17 ont été remportées par le joueur le moins bien classé et 27 par le mieux classé (l’écart n’est pas statistiquement significatif ; p=0,13). On remarque que, sur les 22 rencontres à handicap supérieur à 3, on a 10 victoires du moins bien classé.

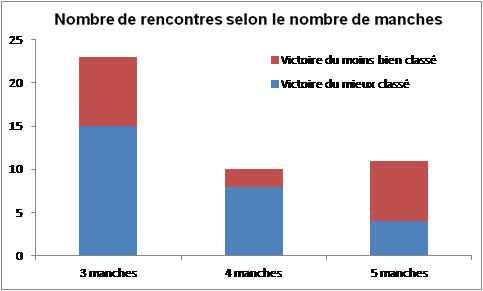
La moitié des rencontres s’est déroulée en 3 manches, un quart en 4 manches et un quart en 5 manches. Les rencontres à faibles handicaps sont les plus disputées.

En l’état actuel, la règle de handicap semble bien adaptée : elle rééquilibre raisonnablement les probabilités de victoire de chaque joueur et ne prolonge pas la durée des rencontres.

BIBLIOGRAPHIE

[1]    Bradley, R.A. and Terry, M.A. (1952). Rank analysis of incomplete block designs. Biometrika, 39, 324-345.

[2]    Binmore K. (1999). Jeux et théorie des jeux. Edition DeBoeck Université.

[3]    Coupet A. et Gerville-Réache L. (2007). Comparison between table tennis scoring systems (11 & 21 points) by probabilistic simulation, The proceedings of the ninth ITTF sports science congress, Beijing, 33-40.

[4]    Sarfati S. et Fegyvères M. (2000). Mathématiques : Méthodes, savoir-faire et astuces. Edition Bréal.

 

Léo Gerville-Réache, Loïc Champagne & Alain Coupet
Les derniers articles par Léo Gerville-Réache, Loïc Champagne & Alain Coupet (tout voir)