Bref historique et paradigme de Shannon
Les codes correcteurs protègent les données des erreurs de transmission dues au bruit thermique, à l’atténuation du signal et à tout autre type de perturbation. Ils sont utilisés dans les téléphones mobiles, la télévision hertzienne, les communications satellitaires, les transmissions par internet ou encore le stockage d’informations numériques. S’il vous est déjà arrivé de rayer un disque compact et de constater que votre lecteur de CD ne parvient plus à lire certaines pistes, il se peut qu’en effectuant une copie du disque (copie de sauvegarde, bien entendu, et uniquement si cela est autorisé), vous constaterez que – pour peu que la rayure soit assez petite – certains graveurs peuvent reconstituer parfaitement la totalité du signal et obtenir un disque à nouveau fonctionnel sur tous les lecteurs ; c’est grâce aux codes correcteurs. Leur invention date de la fin des années quarante et est liée à la théorie de l’information de Claude Shannon ; on pourra (re)lire à ce sujet l’article de Jon D. Paul publié dans Variances.eu (https://variances.eu/?p=2131) ainsi que celui traitant du domaine connexe de la cryptographie (https://variances.eu/?p=3942).
Dans l’article fondateur « A Mathematical Theory of Communication » [1], paru en 1948, Shannon donne une définition mathématique rigoureuse de la notion d’information, prolongeant les travaux de Nyquist (1924) et Hartley (1928). Cette définition s’inspire de l’entropie thermodynamique de Boltzmann et se construit dans un cadre probabiliste. Elle mesure la quantité d’inattendu dans la réalisation d’un phénomène aléatoire ; plus cet évènement est vraisemblable, moins l’information apportée par sa réalisation est élevée. L’unité d’information est le Shannon. 1 Shannon correspond à l’information apportée par la réalisation d’un évènement parmi deux équiprobables. Shannon crée également le modèle générique du schéma de communication (le paradigme de Shannon), différencie la source, le canal de transmission et le rôle du bruit dans la dégradation de l’information. Surtout, il démontre la possibilité paradoxale d’une communication sans erreur malgré la présence de bruit affectant la transmission, pourvu qu’un code approprié soit employé. L’article apporte un nombre impressionnant de nouvelles idées, chacune d’entre elles donnant naissance à une branche des télécommunications. Le lecteur préférant une introduction plus littéraire à la notion d’information pourra se reporter aux premiers chapitres de « l’œuvre ouverte » d’Umberto Eco.
Entre 1947 et 1948, il se passe beaucoup de choses aux « Bell Telephone Laboratories » d’AT&T, dans le New Jersey. A quelques mois (et quelques bureaux) d’intervalle, Shockley, Brattain et Bardeau vont inventer le transistor et plus tard obtenir le prix Nobel de physique pour cette découverte, Claude Shannon va inventer la théorie de l’information et Richard Hamming découvrir les premiers codes correcteurs d’erreurs.
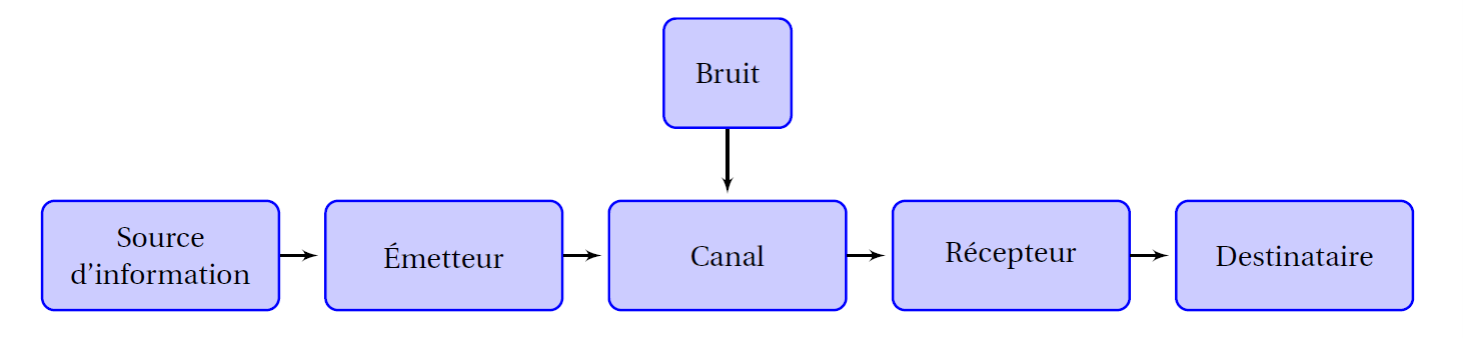
Figure 1 : paradigme de Shannon
Codage de Canal
Dans son article fondateur, Shannon démontre le théorème du codage de canal permettant théoriquement de transmettre des données dans un canal avec une probabilité d’erreur aussi petite que l’on veut, quel que soit le niveau de bruit dans le canal, pourvu que le débit de transmission reste inférieur à un seuil théorique donné : la limite de Shannon. Mais le théorème ne donne pas de méthode de construction et depuis soixante-dix ans, les ingénieur.es et chercheur.es en théorie de l’information s’efforcent de découvrir ces codes et d’atteindre au plus près la limite de Shannon.
Avant de coder le message à transmettre, il faut exprimer celui-ci dans un alphabet adapté au canal de transmission. Le télégraphe de Chappe (1794) utilise un alphabet composé des différentes positions possibles des bras du télégraphe ; après l’invention de l’électricité le code de Samuel Morse (1832) utilise un alphabet ternaire formé de « point », « trait » et « espace ». Avec l’invention de l’informatique et surtout celle du transistor, l’alphabet binaire s’impose rapidement. Le symbole de base est le « bit » (pour binary digit, dénommé ainsi par Tuckey en 1943) qui prend deux valeurs, typiquement 0 ou 1. Mais on peut très bien définir des symboles appartenant à des alphabets pouvant prendre beaucoup plus de deux valeurs. En fait, plus les symboles qui composent l’alphabet peuvent prendre de valeurs différentes, moins le message à transmettre sera long. Par exemple, les symboles peuvent être choisis dans un corps fini, qui est une structure algébrique découverte et étudiée initialement par Evariste Galois (1812-1832). Les corps finis peuvent contenir beaucoup d’éléments, mais dans une structure contrainte : le nombre d’éléments est forcément la puissance d’un nombre premier et la stabilité de l’ensemble par addition et multiplication impose des contraintes fortes entre les éléments. La théorie de Galois a longtemps été considérée comme une curiosité mathématique n’intéressant que les mathématicien.nes pur.es et les amateurs et amatrices d’arithmétique ; elle est aujourd’hui au cœur des modulations codées utilisées quotidiennement en télécommunications.

Figure 2. Un télégraphe de Chappe à Saint-Marcan, Ille et Vilaine
Les codes linéaires
Les premiers codes sont construits de façon algébrique : c’est la redondance d’information qui permet de protéger les messages des erreurs de transmission. Le message à transmettre est transformé en un « mot de code » par adjonction de combinaisons linéaires des bits initiaux. Ceci a pour effet de rendre les symboles du message dépendants les uns des autres. Le mot de code sera donc plus long que le message initial, mais cette redondance est justement ce qui va permettre de détecter et de corriger d’éventuelles erreurs au cours de la transmission.
Lorsque les aviateurs communiquaient jadis avec la tour de contrôle en utilisant un alphabet phonétique (A comme Aline, L comme Louise, L comme Lucien, O comme Octave), c’est une information redondante qui était transmise afin de s’assurer que le contrôleur aérien allait bien comprendre chaque lettre : pour une lettre d’information envoyée, c’est un mot entier qu’il fallait transmettre. Le décodage est alors effectué par notre cerveau qui retrouve par analogie la première lettre d’un prénom familier (parce que dans un mot, les lettres ou les syllabes ne sont pas indépendantes). Le principe est le même pour un code correcteur linéaire. Le mot de code est construit à partir du message initial en le multipliant par une matrice caractéristique du code (la matrice de codage), qui allonge le message en créant des bits redondants, puis la détection d’erreur est effectuée en multipliant le message reçu sur le canal par une autre matrice (la matrice de vérification). Chaque ligne de la matrice de vérification représente une équation liant entre eux les bits transmis. Si un bit est erroné, l’équation correspondante n’est plus satisfaite et en recoupant entre elles toutes les équations non satisfaites, il est possible de détecter l’endroit où l’erreur s’est produite. Si l’alphabet binaire est utilisé, trouver l’endroit où l’erreur s’est produite est équivalent à corriger cette erreur : il suffit de remplacer le 0 par 1 et vice-versa !
Les deux premiers exemples de codes correcteurs sont dus à Richard Hamming et Marcel Golay. Richard Hamming travaillait avec Claude Shannon en 1947. Avant chaque week-end, il lançait ses calculs sur l’ordinateur du laboratoire et revenait en début de semaine suivante pour s’apercevoir que l’ordinateur avait souvent arrêté l’exécution de son programme suite à une erreur. Hamming se disait que si la machine était en mesure de détecter une erreur, elle devait bien pouvoir détecter l’endroit où l’erreur se produisait et, tant qu’à faire, la corriger. Le code de Hamming a ainsi été inventé en 1947 et est référencé dans l’article de Shannon de 1948. Marcel Golay a publié en 1949 les caractéristiques d’un code d’une longueur de 23 bits, dont 12 bits d’information, capable de corriger 3 erreurs par mot, tandis que celui de Hamming corrigeait une erreur pour une longueur de 7 bits dont 4 d’information. L’article de Hamming n’a été publié qu’en 1950, le temps que le dépôt de brevet soit effectué ; s’en suivit une polémique entre Golay et Hamming sur la paternité de l’invention du premier code. Le minitel utilisait un code de Hamming de longueur 128. Le code de Golay a été utilisé dans les sondes Viking dans leur voyage vers Mars, et par la sonde Voyager, lancée en 1979 en direction de Jupiter. À la fin des années 90, Voyager continuait à émettre des messages vers la Terre au-delà de l’orbite de Pluton.
Le pouvoir de correction d’un code (c’est-à-dire le nombre d’erreurs qu’il peut corriger) n’est pas la seule caractéristique importante. Le rendement (rapport entre le nombre de bits du message initial à transmettre et la longueur totale du mot transmis) est un autre facteur important qui caractérise son efficacité. Dans certains canaux peu brouillés (à l’intérieur d’une fibre optique, par exemple) la probabilité qu’une erreur se produise est très faible (de l’ordre de 10-8 ou 10-9) et l’on peut donc se contenter d’un pouvoir correcteur faible pour privilégier le débit de transmission. Par contre, dans certains canaux très brouillés (une communication avec un satellite au fin fond du système solaire, par exemple) il est préférable d’avoir un pouvoir correcteur fort pour bien protéger la communication.
Le pouvoir correcteur est lié à la géométrie du code et à la distance entre deux mots (la « distance de Hamming » est le nombre de coordonnées dont deux mots diffèrent). La distance minimale d’un code est la plus petite distance entre deux mots quelconques. Les mots du code sont dilués au sein de l’espace (très grand) de tous les messages possibles. Plus les mots sont éloignés les uns des autres, meilleur sera le pouvoir correcteur. Un décodage simple (mais optimal au sens du maximum de vraisemblance) consiste à chercher le mot du code le plus proche du message reçu après la transmission. Lorsque la taille des messages est très petite, c’est facile à faire. Mais les codes actuels ont des longueurs de plusieurs dizaines voire plusieurs centaines de milliers de bits et il est alors impossible de procéder ainsi : le décodage algébrique est fortement limité par la dimension.
Dans les années soixante, les mathématicien.nes ont développé des codes plus puissants (corrigeant plus d’erreurs pour une longueur et/ou un rendement donné), comme les codes de Reed et Muller (utilisés par la sonde Mariner pour envoyer des photos de Mars en 1972) ou les codes de Reed et Solomon dont les symboles appartiennent à des corps finis qui peuvent prendre 256, 1024 voire 2048 valeurs différentes pour chaque symbole. Ils sont utilisés dans les disques compacts, dans les DVD, dans les transmissions GSM ou dans le protocole internet ADSL [2]. Ce sont toujours des codes linéaires, mais les techniques de décodage sont plus élaborées et utilisent la transformation de Fourier dans les corps finis ou des propriétés algébriques des espaces en jeu. Mais ces codes restent loin de la limite théorique promise par Shannon et à la fin des années 80, beaucoup de spécialistes pensent que cette limite ne sera jamais atteinte.

Figure 3 : exemple de l’efficacité d’un code de Reed Solomon (Xiaoli Sun – Nasa)
L’invention des turbocodes
Au début des années 1990, trois chercheurs de l’école nationale des télécommunications de Bretagne (aujourd’hui l’institut Mines Télécom Atlantique) présentent des codes dont ils assurent qu’ils sont à quelques dixièmes de décibels de la limite de Shannon. Après plusieurs années de doute, la communauté du codage se rend compte que les « turbocodes » de Claude Berrou, Alain Glavieux et Punya Thitimajshima ont effectivement la puissance de correction annoncée et ils deviennent alors les codes les plus utilisés de l’industrie (communications satellitaires, hertziennes, radio-téléphonie, réseau 4G, stockage des données en informatique, etc.). Les techniques de décodage associées sont statistiques : maximum de vraisemblance, algorithme de Viterbi, utilisation de la notion d’entropie. La qualité du code ne se mesure plus seulement avec la distance minimale, mais en observant le taux d’erreur par bit pour un rapport signal sur bruit donné du canal.
Le principe des turbocodes est le suivant : en réinjectant dans le décodeur un message qui a déjà été décodé (mais dans lequel peuvent encore rester des erreurs résiduelles) on peut bénéficier d’une information supplémentaire et s’en servir pour améliorer le décodage ; de la même façon que dans un moteur de voiture, le turbo utilise les gaz d’échappement afin d’augmenter la puissance du véhicule. En électronique, on parle de boucle de rétroaction. Typiquement, on utilise deux codes différents dans lesquels on fait circuler alternativement les messages (on dit qu’ils sont entrelacés). De la même façon que dans les mots croisés où le fait de trouver un mot horizontal donne des indications sur les mots verticaux, l’alternance des deux décodages permet de gagner de l’information sur les bits et d’améliorer le décodage, grâce à une grandeur appelée « information extrinsèque ». Elle résulte de la différence entre l’information a priori disponible en entrée du décodeur et l’information a posteriori calculée après décodage [3]. « Maximum de vraisemblance », « information a priori », « a posteriori », tous ces termes nous rappellent les cours de statistiques de l’ENSAE…
En caricaturant un peu, on dispose à cette époque de codes algébriques dont on sait démontrer mathématiquement et rigoureusement qu’ils ne sont pas très efficaces, et de codes inventés par des ingénieurs électroniciens de Télécom Brest, qui sont très efficaces mais on ne sait pas bien encore démontrer pourquoi. S’il n’existe pas de démonstration rigoureuse de la grande efficacité des turbocodes, les méthodes de décodage statistique itératives ont des points communs avec les techniques bayésiennes et des analogies avec les réseaux de neurones profonds (eux aussi très efficaces dans la résolution de certains problèmes, sans qu’on sache exactement ce qui se passe à l’intérieur du réseau) … Certains articles de recherche récents s’intéressent aux réseaux de neurones entraînés pour imiter le turbo-décodage.

Figure 4 : un exemple de turbo-décodage (Claude Berrou et Joseph Boutros, ENST)
Références
[1] Claude E. Shannon, « A Mathematical Theory of Communication », Bell System Technical Journal, vol. 27, 1948.
[2] Odile Papini et Jacques Wolfmann, « algèbre discrète et codes correcteurs », Mathématiques et applications, Springer Verlag, 1995.
[3] Claude Berrou, « Codes et turbocodes », Springer, 2007.


Commentaires récents