 Ce livre*, rédigé par deux anciens normaliens professeurs de mathématiques en classes préparatoires, est une vraie réussite, dont le titre annonce bien la couleur. Un avis préliminaire pour préciser un peu : nulle nécessité d’être féru de jeux ou de casse-têtes pour s’y plonger, mais sans appétit pour les mathématiques mieux vaut passer son chemin.
Ce livre*, rédigé par deux anciens normaliens professeurs de mathématiques en classes préparatoires, est une vraie réussite, dont le titre annonce bien la couleur. Un avis préliminaire pour préciser un peu : nulle nécessité d’être féru de jeux ou de casse-têtes pour s’y plonger, mais sans appétit pour les mathématiques mieux vaut passer son chemin.
Un ouvrage mathématique autant que ludique
L’ouvrage, d’une grande qualité éditoriale, est structuré en quinze chapitres et autant de jeux, dont la résolution, ou à défaut l’analyse détaillée, s’appuie sur des concepts mathématiques sous-jacents. Pour faciliter la lecture du plus grand nombre, les auteurs détaillent le contexte historique, décrivent les principes et règles du jeu à l’aide de riches figures et schémas, puis prennent soin de rappeler définitions et résultats mathématiques avant leur mise en œuvre. Dans l’ensemble, la présentation se situe à mi-chemin entre la vulgarisation de recettes plus ou moins obscures et les publications de recherche, avec une progression en douceur du niveau de difficulté. Les exposés et démonstrations sont toujours très détaillés et agrémentés d’abondantes références bibliographiques.
Des jeux qui ont distrait les mathématiciens à travers les âges

Le baguenaudier
La quinzaine de jeux et casse-têtes considérés contient à la fois de grands classiques et quelques exemples moins familiers. Il ne faut y voir ni logique de catalogue, ni souci d’exhaustivité. Le fil directeur de la sélection repose davantage sur l’intérêt suscité par ces divertissements auprès de mathématiciens de différentes époques : du baguenaudier étudié par Jérôme Cardan puis John Wallis, au jeu de Hex cher à John Nash. A plusieurs reprises, des variantes et généralisations sont introduites en raison de nouvelles questions soulevées et de leur intérêt sur le plan mathématique.
L’esprit du livre ne semble pas animé en premier rang par la recherche à tout prix de solutions ou de stratégies gagnantes. La force brute de l’ordinateur ou les algorithmes d’IA ne font d’ailleurs qu’une bouchée de la plupart des dispositifs analysés. L’essentiel réside plutôt dans la quête d’une compréhension profonde des situations, conjuguée à la diversité et la beauté des mathématiques utilisées. Pour beaucoup de casse-têtes, la démarche consistant à jouer un peu au hasard conduit généralement à une certaine frustration. Même en cas de réussite, on n’est pas assuré de comprendre pourquoi ni comment reproduire la résolution.
Les auteurs se concentrent uniquement sur des jeux en solitaire ou à deux joueurs. A quelques exceptions près dans les deux derniers chapitres, le ou les joueurs partagent une information parfaite, le hasard n’intervient pas. Dans ce contexte, les outils utilisés relèvent essentiellement de mathématiques discrètes et de la combinatoire, avec quelques éléments omniprésents :
- L’arithmétique en base 2 ou 3.
- Des structures algébriques finies : groupe des permutations de n éléments, anneau ou corps des entiers modulo n.
- La théorie des graphes.
Une riche source d’inspiration pédagogique
Sans en avoir ostensiblement l’air, l’ouvrage s’avère très formateur et source d’inspiration motivante pour des enseignements de mathématiques et d’informatique. Il présente d’évidentes vertus pédagogiques et d’habileté à manipuler et éclairer des concepts parfois abstraits, pour traiter des questions très concrètes. Par ailleurs, l’art délicat des choix de modélisation est régulièrement mis en évidence : savant mélange de technique, d’imagination et de créativité.
Tour de Hanoï et informatique
En informatique, au-delà de la simple écriture en bits, d’autres codages sont illustrés. Les vieux problèmes de pesées et de détection de fausses pièces, formulés au XVIe siècle, peuvent être résolus avec une décomposition alternée en base 3. Le baguenaudier est à l’origine du code de Gray, code binaire alternatif au code usuel, couramment utilisé en électronique. Une extension en base 3 résout le problème des tours de Hanoï, un grand classique des casse-têtes inventé par Edouard Lucas[1], plébiscité pour introduire et incarner le raisonnement par récurrence et le principe de la programmation récursive. Le jeu de pile ou face, par ailleurs, est l’occasion de manipuler les notions de langages et d’automates.
Jeu de maths, jeu de taquin

Le taquin
En mathématiques, le concept général d’invariant peut être illustré par différents casse-têtes, en s’interrogeant sur les positions atteignables à partir de la position initiale. La plupart du temps les mouvements élémentaires présentent une structure de groupe, avec à la clé toutes les propriétés associées. Un exemple simple est le jeu de taquin, très populaire en son temps, dont l’expression est passée dans le langage courant. Par rapport à la position initiale, le mélange des tuiles s’inscrit dans le groupe des permutations de seize éléments. On voit rapidement à l’aide de la signature d’une permutation comme invariant[2], qu’il est par exemple impossible d’échanger deux tuiles en laissant tout le reste en l’état (transposition). Le cas du solitaire demande davantage d’efforts, avec la construction d’un invariant à partir du corps à quatre éléments F4. On montre alors qu’en commençant par le retrait du pion sur la case centrale, il est possible (impossible) dans le modèle anglais (français) de terminer avec le dernier pion sur cette case.
Rubik’s Cube et théorie des groupes

Le solitaire français
(Le modèle anglais a 4 pions de moins et une forme en croix)
Le Rubik’s Cube s’impose comme le casse-tête mathématique par excellence, en quelque sorte descendant et extension en trois dimensions du taquin. Plus de 50 ans mais pas vieux jeu, l’objet iconique des années 1980 compte toujours de fervents et jeunes adeptes[3]. Avec le taquin ils constituent d’excellents terrains de jeu pour motiver l’étude de la théorie des groupes et s’approprier les notions fondamentales et d’autres plus avancées. Dans les deux cas, l’ensemble des mélanges atteignables correspond à un sous-groupe du groupe des permutations, qu’il s’agit d’expliciter. On rencontre là les passages parmi les plus techniques, mais en retour éclairants sur le produit semi-direct de groupes, la droite projective sur un corps, les homographies.
Une certaine originalité épice le recours à l’algèbre linéaire, avec espaces vectoriels et calcul matriciel sur le corps des entiers modulo 2, moins communs que sur les nombres réels ou complexes. Un large éventail de notions est mobilisé : noyau et image d’applications linéaires, valeurs propres, réduction d’endomorphismes. Ici et là on trouvera également matière à analogie avec la thermodynamique (entropie, irréversibilité) et la physique statistique (verres de spin, modèle d’Ising).
Si une multitude de divertissements récréatifs peuvent être analysés à l’aide d’outils développés auparavant dans d’autres contextes, quelques domaines des mathématiques trouvent également leur origine dans des questionnements d’ordre ludique.
Quand les jeux créent les maths
La première ébauche de théorie des probabilités est généralement attribuée à Pascal et à Fermat, en réponse à des questions soulevées par le chevalier de Méré, joueur impénitent familier des paris basés sur les lancers de dés. Les probabilités sont donc nées au XVIIe siècle en tant que discipline mathématique, à partir de réflexions motivées par des jeux de hasard. C’est une branche relativement jeune des mathématiques, mais à peine moins que la théorie des graphes. La tradition en associe l’éclosion un siècle plus tard au problème des sept ponts de Königsberg posé par Leonhard Euler. Plus près de nous, la théorie des jeux, tout en conservant trace de ses origines ludiques dans son patronyme, s’est considérablement développée au cours du siècle dernier en une discipline relevant autant des mathématiques que de la microéconomie.
Promenade en théorie des graphes
Un chapitre du livre est entièrement consacré à la théorie des graphes et à l’exposé des notions essentielles à partir d’exemples variés. L’utilisation de graphes est très naturelle dans la représentation et l’analyse de la plupart des jeux, dont la brique élémentaire commune est la description du passage d’une position à une autre. Plus généralement, on remarquera que peu de concepts sont d’application aussi universelle, tant dans les sciences de la nature que sociales. Cela donne lieu en informatique à l’élaboration de quantités d’algorithmes [1] pour résoudre en particulier les problèmes spécifiques aux activités de réseaux. De gros théorèmes difficiles comme celui des quatre couleurs ont également suscité l’attention des mathématiciens et conduit au déploiement d’une branche des mathématiques. Le nom de Claude Berge[4] y est couramment associé et apparaît souvent au fil de la lecture. Grand amateur de jeux et divertissements littéraires, il a marqué la recherche et le développement de la théorie moderne des graphes, notamment avec l’introduction des notions de graphes parfaits et d’hypergraphes [2]. On lui doit également des ouvrages majeurs en combinatoire et en topologie (cf. [3] qui n’est pas sans lien avec ce qui suit).
Maths et stratégie
En théorie des jeux, Ernst Zermelo fait figure de précurseur avec un fameux théorème énoncé en 1913 : dans un jeu fini à information complète et sans partie nulle, l’un des deux joueurs a une stratégie gagnante. Résultat d’existence d’une utilité pratique limitée, qui n’exhibe pas de construction de cette stratégie (c’est heureux pour l’intérêt du jeu). Expliciter une stratégie gagnante[5] mène entre autres aux concepts de noyau et de nombre de Grundy dans un graphe. Les jeux de type Nim s’en trouvent à la source, donnant leur nom à la Nim-addition[6] qui permet de calculer leur fonction de Grundy. Un chapitre est dédié à ce type de jeux et à l’identification des stratégies victorieuses. L’idée générique est de créer une partition du jeu en deux, basée sur le nombre de Grundy d’une position : quand elle est dans le noyau, quel que soit le coup joué on sort du noyau ; quand elle est en dehors du noyau, il existe toujours un coup qui y ramène.
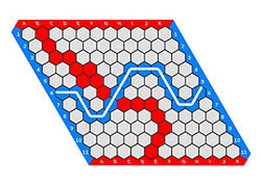
Le jeu de Hex
Le jeu de Hex, apparu dans les années 1940, est aussi intimement lié aux premiers pas de la théorie des jeux. Outre une part de paternité attribuée à John Nash, d’autres grands noms comme Claude Berge et David Gale y portaient également un intérêt particulier. Ce dernier a joué par ailleurs un rôle majeur dans le développement ultérieur de la théorie de l’équilibre général[7]. Cette ouverture vers la modélisation économique[8] dépasse le cadre du livre, mais mérite d’en rappeler les grandes lignes. On peut tirer le fil à partir d’un résultat établi par Gale, d’équivalence entre l’impossibilité d’une partie nulle dans le jeu de Hex et le théorème de point fixe de Brouwer !
Autour du théorème de Brouwer
Les auteurs en donnent une version pour le disque en dimension 2 : Toute application continue dans le plan euclidien, du disque unité fermé (bord inclus) dans lui-même admet un point fixe. Cet énoncé particulier dit néanmoins l’essentiel du théorème standard, valable en dimension finie quelconque et pour des ensembles convexes et compacts (soit en dimension finie, fermés et bornés).
Avec celui de Banach-Picard, le théorème de Brouwer (1912) est sans doute le plus familier de la grande famille des résultats de points fixes. Il compte parmi les outils majeurs de la topologie et de l’analyse non linéaire, aux utilisations multiples dans de nombreux domaines comme l’étude des zéros d’une fonction, l’analyse des équations différentielles, les problèmes d’optimisation. Il a joué un rôle catalyseur dans l’émergence, au cours du siècle dernier, de différentes branches des mathématiques et de l’économie quantitative.
Dès la fin des années 1920, John von Neumann a perçu tout son intérêt pour poser les fondations de la théorie des jeux et aboutir au théorème du minimax. En parallèle, des principes relevant davantage de la combinatoire que dans la démonstration de Brouwer ont été mis en évidence. Le lemme de Sperner (1928) et le « lemme des trois Polonais » (Knaster-Kuratowski-Mazurkiewicz, 1929) offrirent à la fois de nouvelles démonstrations élégantes et des procédés plus constructifs que l’approche originelle de Brouwer, qui garantit l’existence d’un point fixe sans apporter de méthode générale pour le trouver.
Jeux économiques
Il existe diverses variantes et extensions, par exemple dans des espaces de dimension infinie. Le théorème de Kakutani (1941) établit notamment une utile généralisation à des applications multivoques (ou correspondances), particulièrement adaptée aux problèmes de la théorie des jeux et à la modélisation économique. Il a été popularisé par un article[9] et la thèse de Nash en 1950, avec une utilisation suggérée par Gale. Il figure également au cœur des résultats d’existence d’un équilibre général obtenus en 1954 par Kenneth Arrow et Gérard Debreu, et indépendamment par Lionel McKenzie.
Dans cette lignée, deux résultats majeurs se distinguent par la suite ([4] et [5] sont des exposés de référence sur l’ensemble du sujet) :
- Le théorème de Debreu-Gale-Nikaido (1955-56), moyen le plus commode pour démontrer l’existence de solutions dans de nombreux modèles rencontrés en économie.
- L’inégalité minimax de Ky Fan (1972), équivalente au théorème de Brouwer, mais souvent plus maniable.
Dans le livre, l’impossibilité de parties nulles pour le jeu de Hex est démontrée avec un théorème équivalent à celui de Brouwer, dit de non rétraction : il n’existe aucune transformation continue du disque sur sa frontière (cercle), laissant invariants les points de cette dernière. Une image physique est qu’on ne peut pas replier sur le bord la membrane d‘un tambour sans la déchirer.
Un peu de hasard pour finir
Comme souligné plus haut, les auteurs considèrent essentiellement des situations où le hasard n’intervient pas ; ce qui est généralement le cas pour les casse-têtes. Avec plusieurs joueurs, une composante aléatoire s’invite beaucoup plus facilement, de façon intrinsèque (lancer de dés) ou par suite d’une information incomplète comme dans la plupart des jeux de cartes. Ces derniers sont considérés ici uniquement sous l’aspect de leur mélange. Dans un premier temps, le cadre reste purement déterministe avec les faux mélanges qui donnent l’illusion de battre les cartes au hasard et alimentent de nombreux tours de magie. Les suites de de Bruijn[10] sont souvent utilisées comme mécanisme sous-jacent. A l’opposé, les vrais mélanges aléatoires constituent le premier exemple de recours au calcul des probabilités. Le second est le tirage répété de piles ou faces équiprobables et le calcul des temps d’apparition de motifs (séquences données de tirages successifs). Dispositif plutôt basique, mais déjà très riche en paradoxes et propriétés contre-intuitives, avec un avant-goût du singe dactylographe de Borel. Outre les manipulations de base du calcul des probabilités, ces derniers chapitres illustrent l’usage des chaînes de Markov, des séries génératrices et de distances entre lois de probabilités.
Une lecture assez captivante donc, pour revisiter sous un angle ludique et stimulant différents thèmes mathématiques mis en œuvre sur des énigmes plus ou moins classiques et complexes. Elle met en évidence comment de simples passe-temps au charme un peu suranné se révèlent tout autant des points d’entrée vers le raisonnement déductif, des résolutions originales et la pensée abstraite.
Mots-clés : Théorie des jeux – Graphes – Équilibre général.
* « Jeux, casse-têtes et mathématiques » de Yves Dutrieux et Hervé Gianella, aux éditions Cassini
Pour aller plus loin
Quelques pistes plus académiques que ludiques (quoique …).
Deux grands classiques indémodables sur les graphes :
[1] Michel Gondran et Michel Minoux, Graphes et algorithmes, Lavoisier (2009).
[2] Claude Berge, Graphes et hypergraphes, Dunod (1970).
[3] Claude Berge, Espaces topologiques et fonctions multivoques, Dunod (1959).
[4] Jean-Pierre Aubin, L’analyse non linéaire et ses motivations économiques, Masson (1984).
[5] Philippe Bich, Cours d’analyse fonctionnelle et convexe, ENSAE (2008-2009).
Sur la théorie des jeux :
Hervé Moulin, Fondation de la théorie des jeux, Hermann (1979).
Hervé Moulin, Théorie des jeux pour l’économie et la politique, Hermann (1981).
Une approche par la géométrie différentielle :
Yves Balasko, Fondements de la théorie de l’équilibre général, Economica (1988).
Kim C. Border, Fixed Point Theorems with Applications to Economics and Game Theory, Cambridge University Press (1989).
[1] Un pionnier du genre avec ses Récréations mathématiques en 4 tomes parus entre 1882 et 1894.
[2] Il y a aussi un petit parfum de topologie algébrique. A une disposition (topologique) des tuiles on associe la signature (grandeur algébrique). Pour mémoire, toute permutation est le produit d’un nombre soit pair, soit impair de transpositions. On définit sa signature respectivement comme 1 ou -1.
[3] Ouvrage de référence par un illustre professeur de « taupe » de l’époque : André Warusfel, Réussir le Rubik’s Cube, Denoël (1981).
[4] En quelques pages, un hommage de Pierre Rosenstiehl : Claude Berge, ses graphes et hypergraphes, Mathématiques et sciences humaines, 160 (2002).
[5] C’est-à-dire à chaque étape du jeu, une fonction de réponse à chacun des coups possibles de l’adversaire, qui assure la victoire à la fin.
[6] Somme sans retenue en écriture binaire, soit un OU exclusif bit par bit.
[7] Un court papier in memoriam : Monique Florenzano, Two lemmas that changed general equilibrium theory, Games and Economic Behavior (2009).
[8] Pour mémoire l’ouvrage fondateur, bébé d’un génie scientifique et d’un économiste : John von Neumann and Oskar Morgenstern, Theory of Games and Economic Behavior, Princeton University Press (1944). Le concept de noyau y est en particulier introduit.
[9] John F. Nash Jr., Equilibrium Points in N-Person Games, PNAS 36 (1950). Postérieure, la thèse (Non-Cooperative Games, PhD Dissertation, Princeton University, May 1950) renvoie à l’article mais utilise le théorème de Brouwer.
[10] Séquence de 2n bits dont la lecture circulaire par groupe de n bits successifs donne une et une seule fois chacun des mots de n bits.
Crédits images : collection personnelle, sauf jeu de Hex / Wikipedia.


Commentaires récents