Tout comme l’histoire de l’intelligence artificielle est marquée par des avancées majeures et des périodes d’absence quasi-totale, appelées des « hivers », celle des mathématiques « récentes », c’est-à-dire commençant à la fin du néolithique (de 6000 à 3000 ans avant notre ère), est caractérisée également par des hauts et des bas, des avancées ou des reculs.
Nous allons aborder deux périodes de stagnation en Occident, l’une globale suite à la dislocation de l’empire romain et la disparition des bibliothèques, l’autre plus locale en Flandre à l’époque des Pays-Bas espagnols.
Les bibliothèques, lieux de diffusion des connaissances
Les développements dus aux mathématiciens et géomètres mésopotamiens, puis égyptiens sont une réalité. Le plus ancien document mathématique retrouvé date du XVIe siècle avant notre ère, écrit par le scribe Ahmès, qui mentionne d’ailleurs que les résultats retranscrits datent d’au moins trois siècles. Ce volumen contient des résultats d’arithmétique, d’algèbre, de géométrie ; on y trouve la première estimation de π, évalué à 3,16.
Ils ont été suivis par les progrès des Grecs. Comment nier le rôle des travaux de Pythagore et de sa Fraternité, d’Euclide ou de Diophante, se traduisant par des écrits diffusés dans les premières bibliothèques du monde (Alexandrie, Pergame) ?
Ces bibliothèques, vrais centres de savoir, regroupaient les écrits des penseurs et savants reproduits par les scribes sous la forme de volumen (rouleaux) ou de codex (l’ancêtre de nos livres). Leur rôle est fondamental pour l’archivage des connaissances, et aussi pour leur transmission, en tout domaine – théologie, histoire, idées, poésie, théâtre, philosophie, astronomie, etc. ; les mathématiques n’échappent pas à cette règle. Cependant le risque de perte majeure existe aussi : incendie, destruction volontaire ou non, perception variable de leur utilité.
Les bibliothèques d’Alexandrie ont abrité jusqu’à 700 000 ouvrages ; même si les hypothèses sur les causes sont multiples, leur disparition ne peut être niée. Une première étape a lieu en 47 ans avant notre ère lors de l’attaque de Jules César. En 389 le fanatisme religieux intervient indirectement ; l’empereur chrétien Théodose ordonne de détruire tous les édifices « païens », la bibliothèque en fait partie. En 642, enfin, le calife musulman Omar considère que tous les livres contraires au Coran doivent être détruits, et ceux qui y sont conformes sont inutiles et donc également à détruire.
La bibliothèque de Pergame contenait 200 000 œuvres. L’amour entre Cléopâtre et Marc-Antoine permettra à ce dernier de s’y servir amplement pour reconstituer la bibliothèque d’Alexandrie. Ces écrits partiront ensuite soit à Rome, soit à la bibliothèque de Constantinople.
Cette dernière est créée au IVe siècle par l’empereur romain Constantin et développée par son fils Constance II. Elle regroupe peu à peu les savoirs de l’empire romain d’Occident à cause des conséquences des diverses invasions barbares et de la censure due à la religion catholique. Un premier coup d’arrêt est donné en 1204 au moment du sac de Constantinople par les Croisés, accompagné probablement par une destruction des écrits anciens ; le second, définitif, aura lieu à la chute de l’empire byzantin, en 1453, et la prise de la ville par le sultan Mehmed II lors de la conquête ottomane. Les intellectuels fuient vers l’Italie, emportant avec eux une petite partie des écrits.
Cependant, deux innovations majeures vont, au rythme lent de l’époque, influencer la propagation des connaissances.
La première est l’apparition des universités. De premières structures ponctuelles apparaissent en Italie en fin du Xe et début du XIe siècle : Pavie, Salerne. La première université pérenne se trouve à Bologne (pour le droit) en 1088, suivie par Oxford en 1096, en 1150 à Paris par l’Universitas magistrorum et scholarium Parisiensis. Suivront Cambridge en 1209, Salamanque en 1218, Padoue en 1222, Naples en 1224, Toulouse en 1229, la Sorbonne en 1253, Montpellier en 1289 (médecine). Les bibliothèques se recréent, mais les sciences ne sont pas, alors, un domaine universitaire recherché. La part belle est réservée au droit, à la théologie, à la médecine et aux lettres. Il faudra attendre 1619 pour voir la création, à Oxford, d’une chaire mathématique.
La seconde innovation, au milieu du XVe siècle, correspond à l’apparition de l’imprimerie : les premiers travaux de Johannes Gutenberg datent de 1436, à Strasbourg. Au cours des années 1438-1454, il conçoit un ensemble global, un vrai « process industriel » : impression et typographie s’appuient sur la technique de production des caractères métalliques mobiles, la presse à bras et l’encre d’impression. C’est une véritable rupture pour la reproduction des « vrais livres imprimés », répliques en multiples exemplaires et à l’identique d’un original et non plus sa recopie manuelle.
L’apparition du goût du secret chez les mathématiciens
La mathématique, et ses adeptes, contribuent à la compréhension du monde depuis la Mésopotamie jusqu’à l’avènement de Rome, notamment en géométrie et en arithmétique orientées vers les applications, avec de premiers ouvrages fondamentaux dont peu nous sont parvenus, notamment pour les raisons mentionnées auparavant. La chute de l’empire romain marque un recul des mathématiques occidentales qui va durer près de mille ans ; mais parallèlement, les écoles des mathématiciens indiens et perses, dans la deuxième partie du premier millénaire, vont connaître de brillantes avancées. L’invention du zéro (également connu des Mayas) et des symboles des chiffres nous viennent de l’Inde, et les mathématiciens perses ont, entre autres, fait naître l’algèbre ; le grand Al-Khwârizmî (né vers 780, mort vers 850) a donné son nom – latinisé – au concept d’algorithme. L’occupation musulmane en Andalousie va permettre aux mathématiques de revenir lentement en Europe.
Dans ce domaine, l’Occident va connaître une longue nuit pendant tout le Moyen-Age, avant que les échanges avec l’Orient ne lui redonnent de la vigueur à partir de la Renaissance. Pourtant de grands noms existent du Xe au XVIe siècle. Gerbert d’Aurillac, formé en Espagne, pape de 999 à 1003, introduit la numération décimale en chiffres indo-arabes. Bien plus tard, Nicolas Chuquet (1445 – 1488), Jacques Peletier du Mans (1517 – 1582), Jacques Aleaume (1562 – 1627) ou encore François Viète (1540 – 1608) mériteraient d’être bien plus connus et considérés. En Italie, citons Niccolo Tartaglia (1499 – 1557) ou Jérôme Cardan (1501 – 1576).
De plus, les travaux des mathématiciens sont le plus souvent secrets car orientés vers la pratique : Tartaglia a résolu les équations du troisième degré, en donne très confidentiellement la solution à Cardan qui les publie dix ans plus tard, ce qui créera un scandale.
Les découvertes de chacun sont fréquemment vendues aux commerçants, comptables, financiers pour résoudre leurs problèmes et donc non divulguées. Il faudra attendre l’abbé Marin Mersenne (1588 – 1648), par ailleurs grand théoricien des nombres, pour voir naître les échanges et la communication entre mathématiciens parisiens, français, étrangers, et son groupe créé en 1638 sous le nom d’Academia Parisiensis sera à l’origine de l’Académie des Sciences, fondée en 1666, un peu après la Royal Society anglaise (1645). A partir du XVIIe siècle, la corporation des mathématiciens (Fermat, Roberval, Pascal, Gassendi, Huygens, etc.) va prendre un virage décisif par l’habitude de se parler, de dialoguer, de construire ensemble. Ainsi Pierre de Fermat rédige très peu de démonstrations de ses résultats ; son célèbre théorème « 
où x, y et z sont des entiers, est impossible dès que n > 2 » est seulement énoncé en 1637 et ne sera démontré qu’en 1993 par le mathématicien anglais Andrew Wiles. Et pourtant les « entiers des triplets pythagoriciens » vérifiant la relation pour n = 2 sont connus depuis Babylone et mille ans avant Pythagore. Fermat travaille avec Pascal pour jeter les bases du calcul des probabilités, suite à une question d’Antoine Gombaud, le chevalier de Méré ; il correspond également de façon régulière avec l’anglais John Wallis (1616 – 1703), célèbre pour ses intégrales.
Les mathématiciens belgo-flamands-hollandais : l’exemple de Stevin et Snell
Un autre exemple de recul, local celui-ci, vient de la politique. Le territoire formé maintenant par la Belgique, le Luxembourg, les Pays-Bas et le nord de la France devient en 1556, par jeux d’héritages et de successions, les « Pays-Bas espagnols » sous l’autorité de Charles-Quint puis de son successeur Philippe II. Ils demeureront jusqu’en 1713.
Côté violence, cette « occupation » est marquée par une guerre de Quatre-Vingts ans, qui s’étendra de 1568 à 1648 et conduira à l’indépendance de sept provinces du nord, les « Provinces Unies » ou Pays-Bas actuels.
Cette région, notamment la Flandre, est caractérisée par de nombreux scientifiques, en astronomie, médecine, physique, mathématiques, cartographie. Adriaan van Roomen (1561 – 1615) est né à Louvain, Michel Coignet (1549 – 1623) est d’Anvers, Ludolph van Ceulen (1540 – 1610) est allemand mais émigre à Anvers, Govaert Wendelen (1580 – 1667) est originaire du Limbourg, Geert de Kremer (1512 – 1594) est né à Beveren. Nombreux sont ceux dont le nom est latinisé, ce qui assure une visibilité à leurs travaux et écrits : ainsi, van Roomen est Adrianus Romanus, Wendelen est Vendelinus, de Kremer devient le célèbre Gerardus Mercator.
Pour apprécier les avancées dues à cette école néerlando-flamande, nous allons mettre en évidence deux noms, dans l’ordre alphabétique : Willebrord Snell van Royen, (1580 – 1626) et Simon Stevin (1548 – 1620).
Snell, encore appelé Snellius, semble-t-il avec son accord, est né dans la province d’Utrecht et à vécu à Leyde. Fils d’un mathématicien renommé, il a découvert en premier (1621) la loi de la réfraction de la lumière lorsqu’elle change de milieu. Descartes publiera cette loi en 1637, en annexe de son Discours de la méthode. La loi de la réfraction porte d’ailleurs le nom de loi de Snell-Descartes ; sur ce point, pour être complet, la réfraction est déjà présente dans les travaux des mathématiciens arabo-persans du Xe siècle. L’ouvrage majeur de Snell, en latin, s’intitule Erathostenes Batavus de terrae ambitus vera quantitate. Il est publié en 1617, et il y détaille les opérations géodésiques entreprises pour mesurer l’arc de méridien compris entre sa ville, Leyde, et Soeterwoode, dénommée maintenant Zoeterwoude, en Hollande du sud. Il s’agit de la première utilisation en vraie grandeur de la méthode de triangulation, qui sera ensuite amplement employée à partir du XVIIe siècle par Jean Picard ou la famille Cassini, et qui sera à la base de la mesure du mètre par Delambre et Méchain sous la Révolution française via le méridien Dunkerque – Barcelone.
Le principe de la triangulation d’un triangle ABC consiste à déterminer la position du point A, inconnu ou inaccessible, en connaissant la position des deux autres points B et C. En notant par A, B et C les angles et a, b et c les longueurs des côtés opposés, la distance BC = a et les angles B et C sont mesurables et mesurés.
La position du point A est définie par les longueurs BA et/ou CA par application de la relation trigonométrique marquée par la constance du rapport entre une longueur et le sinus de l’angle opposé, formule des mathématiques persanes du XIe siècle :
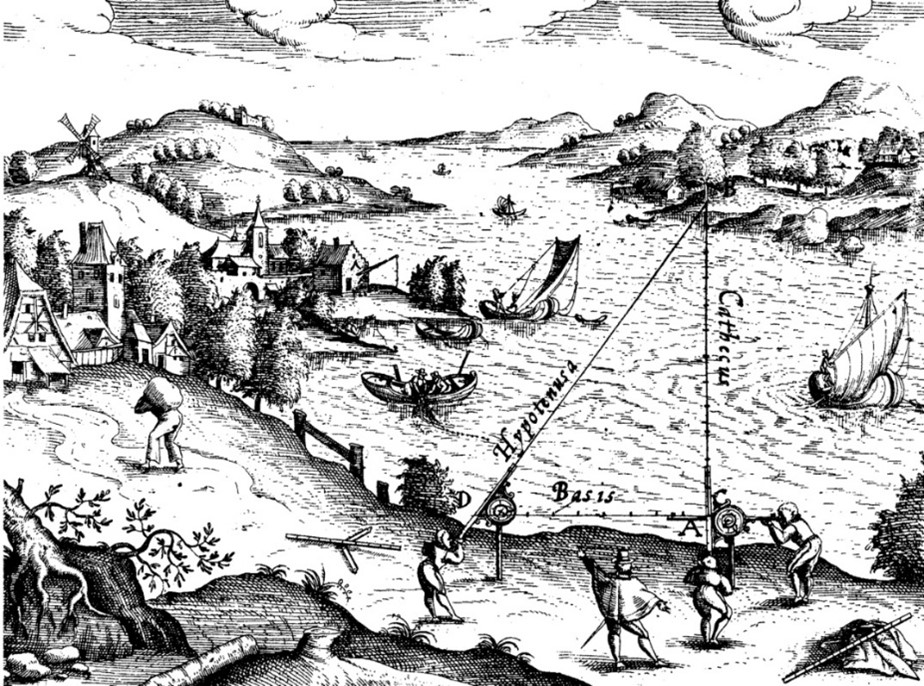
Le principe de la triangulation (Dom. Public)
(Levinus Hulsius, 1550-1606)
Né à Bruges quelques années avant Snell, Simon Stevin est un mathématicien et physicien, spécialiste de mécanique et d’optique. Nous lui devons un système de notation décimale dès 1585 : le nombre que nous écririons maintenant 26,547 était écrit par Stevin 
.
Il emploie des ronds avec des chiffres à l’intérieur ; le 0 remplace « notre » virgule, les 1, 2, 3 etc, positionnent les décimales : première, deuxième et troisième décimale.
Stevin est d’origine comptable, domaine dans lequel il applique avec succès son système. Il publie sa généralisation décimale dès le XVIe siècle en comptabilité, dans un livre nommé Die Thiende (La Disme) publié en 1585 à Anvers chez l’éditeur anversois Christophe Plantin. Il plaide également pour l’application de la base dix aux poids et mesures, deux siècles avant la Révolution française.
Couverture de Die Thiende de Stevin
Il s’éloigne de la comptabilité, s’occupe de travaux sur les fortifications, comme Vauban, devient professeur de mathématiques intéressé par l’algèbre et les applications en physique : mécanique et hydrostatique. Il est le premier à résoudre le problème de l’équilibre d’un corps placé sur un plan incliné ainsi que le paradoxe de l’hydrostatique qui consiste, en mécanique des fluides, à énoncer l’indépendance de la pression et de la forme du récipient contenant le fluide. Ce paradoxe est souvent, à tort, attribué à Blaise Pascal, qui le mentionne dans un ouvrage publié en 1651, donc bien plus tardivement. Il invente également un char à voiles propulsé par le vent, capable de transporter 30 personnes à la vitesse de 40 km/h.
Alors que Snell a accepté de publier en latin, Stevin va adopter une posture proche de la non-violence, à mettre en exergue car fort rare. Il se refusera toujours à écrire ses travaux en latin, jugé trop proche du langage de l’occupant espagnol, et ne publiera qu’en flamand-néerlandais pour défendre cette langue, sa langue. Il faut convenir que ce choix n’a pas aidé à faire connaître ses remarquables travaux. Après sa mort, ils seront traduits en latin par Snell et en français par le mathématicien lorrain Albert Girard (1595 – 1632), et imprimés en 1625 et 1634 par l’éditeur Jacques Elzevier, à Leyde.
Hélas, trop tard : le XVIIe siècle est déjà bien entamé et ses mathématiciens ont pris de nouvelles habitudes qui ne se perdront pas.
Mots-clés : Mathématiques – Histoire – Snell – Stevin
- Deux exemples d’hivers des mathématiques en Occident - 25 juin 2025
- Des grands noms de l’histoire des technologies des médias radio et télévision - 15 juillet 2024
- Des grands noms de l’histoire d’internet - 7 mars 2022
Commentaires récents