Estimation de cotes au football

Introduction

Cet article est issu d’un projet de statistiques appliquées consacré au calcul des estimations de scores au football : estimation de la probabilité d’une victoire, d’un match nul, ou d’une défaite lors d’un match. Le projet a été encadré par Alexander Buchholz et Vincent Cottet.

---

Compte tenu du développement du marché des jeux et des pronostics, divers travaux ont été effectués à ce sujet au cours des dernières années. On pourra lire par exemple l’interview de Jean-Louis Foulley, dans Variances (mai 2017). Deux publications ont particulièrement attiré notre attention, notamment car elles utilisent deux modèles proches mais utilisent deux approches différentes ; il s’agit :

• des travaux de Dixon et Coles, qui optent pour une approche fréquentiste (Mark J. Dixon, Stuart G. Coles, Modelling Association Football Scores and Inefficiencies in the Football Betting Market, Journal of the Royal Statistical Society : Series C (Applied Statistics), 46(2), 1997
• des travaux de Baio et Blangiardo qui utilisent plutôt une approche bayésienne (Gianluca Baio, Marta Blangiardo, Bayesian Hierarchical Model for the Prediction of Football Results, Journal of Applied Statistics, 37(2), 2010.

L’objectif du projet est de comparer les résultats obtenus par ces deux approches à partir d’un même modèle et sur les mêmes données, et donc pouvoir estimer les cotes lors d’un match de football.

1. Présentation des données

Nous nous intéressons aux résultats de la saison 2015-2016 de la Ligue 1 de la Ligue Nationale de Football (auparavant appelé championnat de première division française de football).

Nous nous concentrons uniquement sur les scores finaux de chaque match.

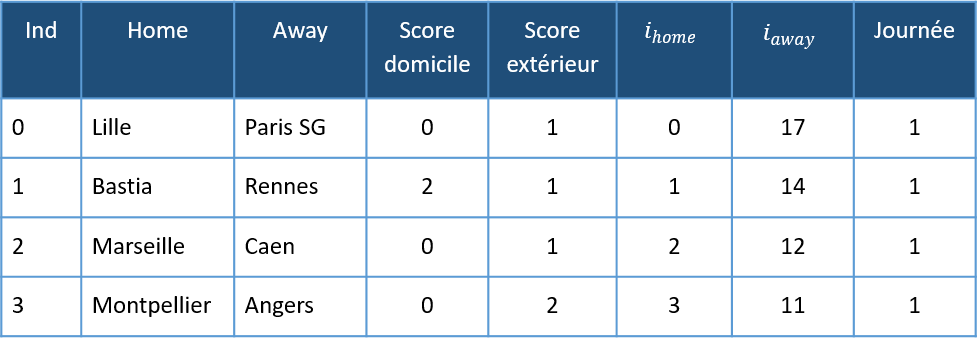
Chaque ligne du tableau de données correspond à un match. Le championnat de Ligue 1 étant constitué de 20 équipes, chaque couple d’équipes se rencontrant deux fois (une fois à domicile et une fois à l’extérieur), le tableau est constitué de 380 lignes.

Chacune des équipes est indicée ( et  ), et la colonne “Journée” correspond au numéro de la journée où a eu lieu ce match.

Par exemple, la première ligne correspond au match Lille – Paris SG, match de la première journée se jouant à Lille, match gagné par le PSG sur le score de 1 à 0.

2. Le modèle utilisé

Nous allons décrire notre modèle.

Soient un match opposant deux équipes i et j, i jouant à domicile et j à l’extérieur. Tout comme les deux articles cités en référence, nous faisons plusieurs hypothèses majeures :

• A chaque match, le nombre de buts marqués par l’équipe à domicile, noté  et ceux marqués par l’équipe à l’extérieur, noté , sont indépendants.
• Chaque équipe i possède un paramètre d’attaque noté  et un paramètre de défense noté . Plus le paramètre  est élevé, plus l’équipe a de chances de marquer un but. Tandis que plus le paramètre de défense  est élevé, plus l’équipe encaisse de buts.
• Un autre paramètre A décrit l’avantage d’une équipe à jouer devant son public (cf point suivant).
• La distribution des buts suit une loi de Poisson :

où

 

Afin de rendre le modèle identifiable, nous y ajoutons la contrainte suivante :

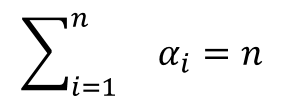
où n est le nombre d’équipes de la ligue (n = 20).

3. L’approche fréquentiste

L’approche fréquentiste est celle adoptée par Dixon et Coles dans leurs travaux. Elle consiste à calculer la log-vraisemblance du modèle, et de calculer les estimateurs de façon à la maximiser :

avec :

Ainsi nous obtenons des estimateurs des paramètres  et  pour chacune des équipes, et du paramètre A.

Nous calculons également l’information de Fisher qui permet de faire une approximation des écarts-types des estimateurs des paramètres. Nous avons également fait le calcul des probabilités du score de chaque match par cette approche, qui permet d’obtenir les probabilités de victoire/nul/défaite. Il s’en suit la possibilité d’établir des cotes que nous pouvons par la suite comparer à celles établies par les bookmakers.

4. L’approche bayésienne

L’approche bayésienne, quant à elle, est utilisé par Biao et Blangiardo dans leur article. Comme le nombre de données utilisées est somme toute assez faible, l’approche bayésienne présente l’avantage d’avoir des écarts-types plus faibles que l’approche fréquentiste.

Nous nous basons sur des méthodes de Monte Carlo afin d’obtenir les estimations des paramètres. Les lois a priori des α_i et β_i et  sont des lois log-normales, et les moyenne et les écarts-types de ces lois a priori des  et  et A suivent respectivement des lois normale et gamma. Nous faisons ainsi une estimation de la loi a posteriori qui nécessite, compte tenu de la difficulté à la calculer, une estimation par l’algorithme de Metropolis-Hastings.

De même, nous calculons également les probabilités de résultat de chaque match.

5. Résultats

Les estimations des différents paramètres d’attaque et de défense pour chaque équipe conduisent à des résultats très similaires entre les deux approches.

Une différence apparaît au niveau des écarts-types, beaucoup moins élevés pour l’approche bayésienne.

Pour la paramètre A :

Pour les paramètres  et  :

Nous observons ainsi que les estimations sont très proches selon les deux approches. La différence majeure porte sur les écart-types, avec une approche bayésienne plus précise. Nous pouvons notamment observer que le PSG, qui a largement dominé la Ligue 1 lors de la saison 2015-2016, a le paramètre  le plus élevé et le paramètre  le plus faible. C’est l’inverse pour Troyes qui a terminé dernier.

Nous avons également pu calculer les probabilités de score selon les deux approches. En voici un exemple pour le match Angers – Toulouse :

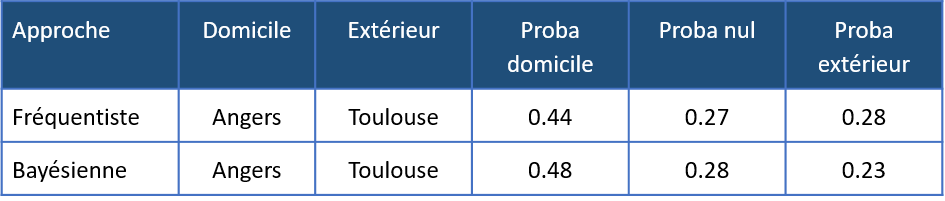
Il est donc possible de calculer les cotes pour chaque match, à travers les deux approches les plus utilisées, qui conduisent à des résultats globalement comparables.

Pour conclure, nous avons étudié deux pistes d’approfondissement. La première a consisté à étudier une stratégie de pari sportif sur les matches, basée sur l’espérance de gain. Une seconde est d’entrer dans le détail de la réalité d’une saison de championnat de football par l’intégration de variables exogènes : par exemple, quel impact sur les paramètres du modèle peut avoir un changement d’entraîneur en cours de saison, ce qui est une pratique non rare. Plus généralement, peut-on intégrer d’autres variables exogènes comme les achats ou ventes de joueurs au mercato d’hiver ?