Colloque « Intelligence Artificielle : fiction ou actions ? » : Les évolutions mathématiques de la science des données

Exposé de Marco Cuturi, Professeur ENSAE-CREST

(Retranscription de Philippe Tassi)

---

Cet exposé constitue une suite tout à fait cohérente à celui du professeur Saporta, car centré sur l’apprentissage non supervisé. Mon propos abordera deux thématiques : d’une part les modèles génératifs, en anglais les generative models, qui font actuellement un quart des interventions dans les conférences portant sur le machine learning ; d’autre part, le transport optimal, problématique de prédilection de Cédric Villani qui en est l’ambassadeur depuis de nombreuses années. C’est un sujet qui remonte très loin dans l’histoire des mathématiques en France, jusqu’à Gaspard Monge (1746 – 1818). Le transport optimal, issu des mathématiques pures, est utile pour résoudre le problème des modèles génératifs, très à la mode en machine learning.

Les modèles génératifs

Commençons par réintroduire l’estimation de densité.

La difficulté de l’estimation de densité est la dimension de l’espace qui contient les points observés, qui peut être extrêmement grande. Le rôle du statisticien est de résumer l’information contenue dans l’échantillon observé. Pour cela, il dispose, dans son arsenal, de l’ensemble des modèles paramétrés. Par exemple, il pourra conclure que les observations sont distribuées selon une densité de la famille des lois gaussiennes multivariées. Dans cette famille, l’idée est de trouver la loi qui semble le mieux se rapprocher des données.

L’un des critères principaux pour procéder à ce calcul a été introduit par Sir Ronald Fisher (1890 – 1962), au début du XX^ème siècle, dans un article intitulé « On an Absolute Criterion for Fitting Frequency Curves », publié en 1912 dans Messenger of Mathematics. Dans cet article, Fisher expose la méthode du maximum de vraisemblance.

Pour des données (x_i), i = 1 à n, et une classe de densités P_θ, θ étant un vecteur de paramètres, on veut déterminer les paramètres maximisant le logarithme de la vraisemblance, c’est-à-dire la somme des logarithmes des P_θ(x_i). Une remarque : on a l’habitude d’utiliser le maximum de vraisemblance avec les modèles simples, comme les modèles gaussiens, qui couvrent tout l’espace ; P_θ(x_i) est donc toujours positif. Si P_θ(x_i) = 0, le logarithme est – ∞, ce qui pose éventuellement problème.

Le maximum de vraisemblance peut s’interpréter aussi de manière géométrique. L’idée est de rechercher le vecteur θ minimisant la divergence au sens de Kullback-Leibler, KL, entre la mesure empirique ν associée aux données, ν = [Σ_i=1àn δ(x_i)]/n où δ est le symbole de la masse de Dirac, et l’ensemble des densités gaussiennes, par exemple. On a donc à résoudre un problème de minimisation :

Min_θ KL(ν, P_θ)

L’objectif est bien de chercher le modèle de probabilité le plus proche des données.

Mais que se passe-t-il en pratique quand cette démarche d’estimation de densité est réalisée dans une dimension plus élevée que 2, par exemple en dimension 3 ? Tout devient plus compliqué. C’est possible, évidemment, avec des lois gaussiennes car les ellipsoïdes définissent les niveaux de densité. Mais des lois plus complexes posent problèmes.

Mais là où les vraies difficultés commencent, c’est quand les points ne sont plus en faible dimension 3, 4, ou même 100, mais 30 000.

Pour un nuage de points comme celui représenté ci-dessus, qui est dans , la question est déjà complexe. Mais supposons que l’on y insère par exemple des images ou des photos qui sont des vecteurs de dimension 30 000 (images de 100 x 100 pixels, où chaque pixel contient trois valeurs) ; comment faire de l’estimation de densité en dimension 30000 ?

Plusieurs approches sont alors envisageables. Estimer une loi gaussienne en dimension 30 000 sera impossible. Une manière simple est d’essayer de réduire la dimension des observations pour pouvoir définir des modèles sur ces représentations en plus basse dimension. Cette approche est très classique, mais elle empêche pratiquement de tirer aléatoirement des images. Vers 2013-2014, les communautés machine learning ont proposé de paramétrer ce problème de manière différente : le point de vue génératif.

Une remarque préalable : nous allons, dans ce qui suit, employer souvent le mot image ; rappelons que ce mot a un sens en mathématiques, image d’un espace par une fonction, et un autre sens en langage courant : image comme un dessin ou, ici, une photo. Le contexte de chaque phrase permet de distinguer chacun des deux sens.

L’approche générative est la suivante : partant toujours des données (x_i), i = 1 à n, ou de leur loi empirique ν, d’une dimension très grande, il ne s’agit plus de définir la loi P_θ la plus adaptée, comme précédemment. Le principe consiste à passer par un espace latent, une variété de dimension très inférieure. Par exemple, un espace latent de dimension 10 ou 100 alors que l’espace originel des données est de dimension 30 000. Le problème d’estimation dans un cadre génératif n’est plus d’estimer P_θ, c’est-à-dire une densité sur l’espace de toutes les images possibles de 100 x 100 pixels, mais plutôt d’estimer une fonction f_θ de l’espace latent dans l’espace des données ; l’idée est ainsi que l’image – au sens fonctionnel du terme – via f_θ de l’espace latent ne couvre pas forcément l’ensemble des données, mais en soit le plus proche possible ; dit autrement, f_θ ne peut pas être une surjection.

Ce principe est très utilisé par exemple pour la génération d’images – au sens photos –. Le paramètre θ sera choisi pour que l’espace s’adapte assez bien aux données. Pour cela, il est nécessaire de disposer d’une formule mathématique qui quantifie la ressemblance entre la variété définie par f_θ et le nuage de points.

Le réflexe statistique le plus fréquent serait de recourir à la bonne vieille formule du maximum de vraisemblance. Malheureusement, la situation évoquée au début de ce paragraphe est ici bien réelle, puisque si, par exemple, une loi gaussienne en dimension 3 remplit tout l’espace et donc tous les points de R³ ont une probabilité positive, même si elle est très faible, dans le cas présent le modèle ne va pas être capable de générer toutes les observations fournies. L’approche va être totalement géométrique pour calculer la distance entre une variété et un nuage de points.

L’innovation apportée dans les années 2013-2014 a été de formuler cette question comme un problème de classification. Je renvoie à la littérature, sur ce point, et plus précisément aux GAN, les Generative Adversarial Networks.

L’approche géométrique proposée consiste, pour quantifier la différence entre la variété et le nuage de points, à trouver des bonnes métriques Δ entre mesures de probabilité. Depuis les années 70, de nombreuses publications préconisent de ne pas faire du maximum de vraisemblance. Sur le choix de Δ, citons, à titre d’exemples, Minimum Chi-Square, not Maximum Likelihood, de Joseph Berkson, Annals of Statistics, 1980, Minimum Hellinger Distance estimation for Poisson mixtures, de Dimitris Karlis et Evdokia Xekalaki, Computational Statistics and Data Analysis, 1998 ; en 2006, un article recommande les estimateurs dits de Kantorovich, qui sont des estimateurs de transport optimal : On mimimum Kantorovich Distance Estimators, Federico Bassetti, Antonella Bodini, Eugenio Regazzini, Statistics and Probability Letters, 2006.

Pour les modèles génératifs, il faut mentionner par exemple MMG GAN : Towards Deeper Understanding of Moment Matching Network, de C-L. Li, W-C. Chang, Y. Cheng, Y. Yang, B. Poczos, 2017, ou Training Generative Neural Networks via Maximum Mean Discrepancy Optimization, Gintare Dziungaite, Daniel Roy, Zoubin Ghahramani, 2015, Wasserstein Training of Restricted Boltzmann Machines, Grégoire Montavon, Klaus-Robert Müller, Marco Cuturi, 2015, Inference in Generative Models using Wasserstein distance, E. Bernton, M. Gerber, P. Jacob, Ch. Robert, 2017, ou encore Wasserstein GAN, Martin Arjovsky, Soumith Chintala, Léon Botton, 2017, Learning Generative Models with Sinkhorn Divergences, Aude Genevay, Gabriel Peyré, Marco Cuturi, 2017, Improving GANs Using Optimal Transport, Tim Salimans, Han Zhang, Alec Radford, Dimitris Metaxas, 2018. Parmi les auteurs, des universitaires, et aussi des membres du Facebook AI Research, comme Léon Botton.

Le transport optimal

La transition est donc faite avec la deuxième thématique de la présentation : le transport optimal. L’idée est d’utiliser la distance dite de transport optimal entre mesures de probabilité pour comparer la proximité entre les données et la variété.

Qu’est-ce que le transport optimal ?

Comme dit en introduction, c’est un sujet initialement très français, même s’il est maintenant mondial. L’initiateur a été Gaspard Monge, au XVIIIe siècle ; cependant, pendant presque un siècle et demi, le transport optimal n’a plus suscité l’intérêt des mathématiciens. Monge a soulevé un problème que personne n’arrivait à résoudre.

Au cours de la seconde guerre mondiale, l’idée du transport optimal est devenue cruciale, la guerre montrant l’importance de la logistique, sur tous les plans. Des progrès majeurs ont alors été réalisés notamment par Leonid Kantorovich et Tjalling Koopmans, qui ont reçu le prix Nobel d’Economie près de trente ans plus tard, en 1975. D’autres auraient peut-être mérité la même récompense, comme George Dantzig qui a résolu le problème posé par Kantorovich. Plus près de nous, mentionnons Cédric Villani (Médaille Fields en 2010) très connu pour ses travaux et livres dans le domaine (Topics in Optimal Transportation, American Mathematical Society, 2003 ; Optimal Transport : Old and New, Springer, 2009).

Les photos qui suivent mettent à l’honneur divers contributeurs à l’avancée du transport optimal.

Pour les data scientists, le transport optimal peut être vu comme une distance sur l’espace des mesures de probabilité, très différente des distances classiques comme celles d’Euclide ou Kullback-Leibler. Tout modèle statistique repose sur une mesure de probabilité.

Un exemple simple et intuitif est constitué des bags of words, les sacs de mots. Dans l’analyse d’un texte, plutôt que d’essayer de comprendre la complexité grammaticale du mot et la linguistique, il est facile de comparer deux styles de textes. Un « sac de mots » est une mesure de probabilité sur l’espace des mots.

Dans les phénomènes naturels, ce qui est observé peut être quantifié de manière probabiliste : regarder une tache plutôt que voir un point localisé. Cette approche est utilisée pour tout ce qui est étude du cerveau.

En pratique, pour illustrer par quelques exemples, le transport sera utile pour comparer deux sacs de mots, avec accès à une géométrie pertinente sur les mots, ou pour comparer deux histogrammes d’activation sur le cortex, sous réserve d’une distance entre deux points d’un cortex.

La géométrie du transport optimal est intéressante parce qu’elle induit des outils très différents de ceux auxquels nous sommes habitués. La distance du transport optimal est la distance de Wasserstein (introduite en 1969 par le mathématicien russe Leonid Wasserstein).

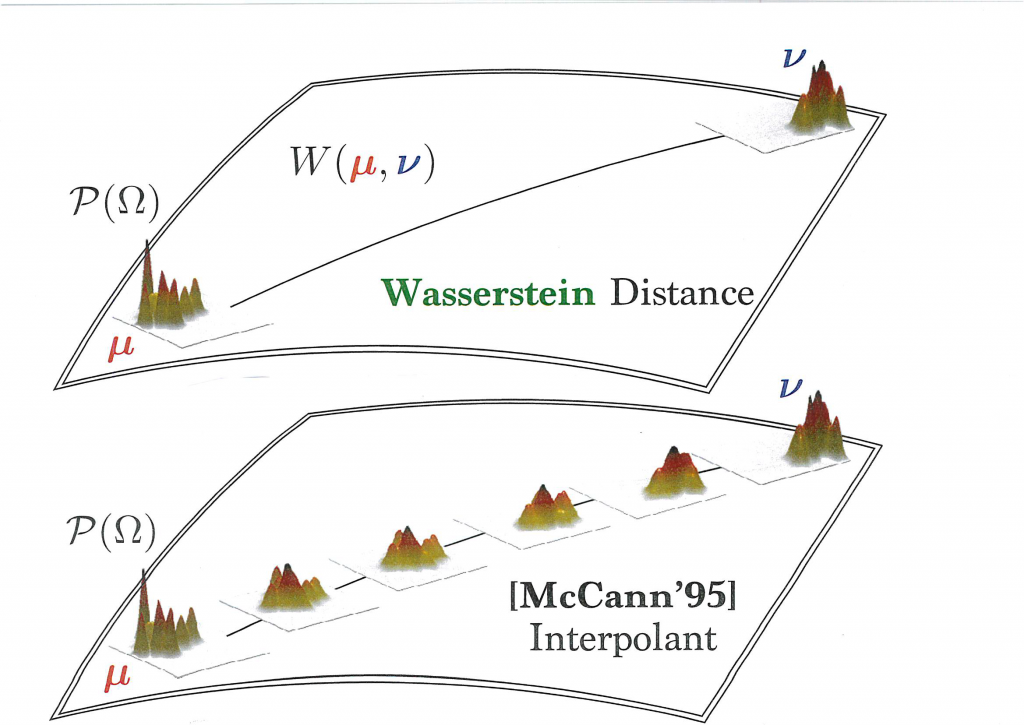
Les graphes ci-dessus illustrent la transition entre deux mesures de probabilité, avec les calculs d’interpolation – une innovation de Robert McCann (université de Toronto) – permettant d’obtenir une série de mesures de probabilité reliant la mesure initiale et la mesure finale.

Nous sommes loin d’Euclide, pour qui la moyenne de deux mesures de probabilité est simplement leur somme divisée par deux, approche strictement linéaire.

Le transport optimal fait bouger la masse de manière latérale à travers l’espace d’observation, ce qui conduit à des interpolations très différentes. Imaginons que nous disposons de trois mesures de probabilité donnant de l’information sur un phénomène physique, et que nous voulions les agréger, les fusionner, problématique très courante. La manière naïve est de les sommer et de diviser par trois.

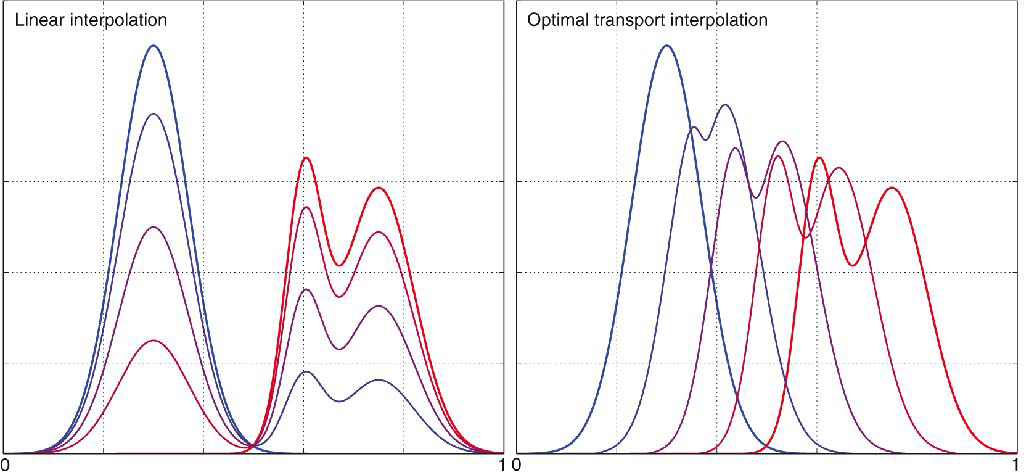
L’interpolation en transport optimal consiste à déplacer la masse. Cette interpolation a du sens en particulier pour tout ce qui est graphique ou image. L’idée est de faire l’interpolation de formes de manière totalement agnostique, c’est-à-dire sans paramétrer une forme. La théorie du transport optimal mène à une sorte d’interpolation entre ces trois formes alors qu’aucune connaissance a priori n’a été apportée sur les formes. La seule information utilisée est la mesure de la distance entre les pixels.

Un peu de mathématiques : quel est le problème initial de Monge, à l’origine du transport optimal ? Monge a exposé ses idées de transport au XVIIIe siècle, à partir de la question suivante : disposant d’un tas de sable, d’un certain volume, et d’un trou, quelle est la manière optimale pour déplacer le tas de sable vers le trou et le remplir ?

Au XX^ème siècle, il aurait suffi de prendre un tracteur et de pousser le sable vers le trou sans se poser la question de l’optimalité quant à la manière de réaliser ce transport. En 1781, le problème est bien sûr complètement différent car seul un ouvrier peut intervenir, muni de sa seule pelle, cet ouvrier devant transporter la masse de sable élément par élément et d’un endroit à l’autre.

Le problème de Monge consiste à demander à un ouvrier muni d’une pelle de transporter la masse de sable μ, située à un endroit E couvrant divers points x, en un autre point y = T(x), en lui précisant tous les points par lesquels l’ouvrier doit passer et le point T(x) où il doit amener cette masse.

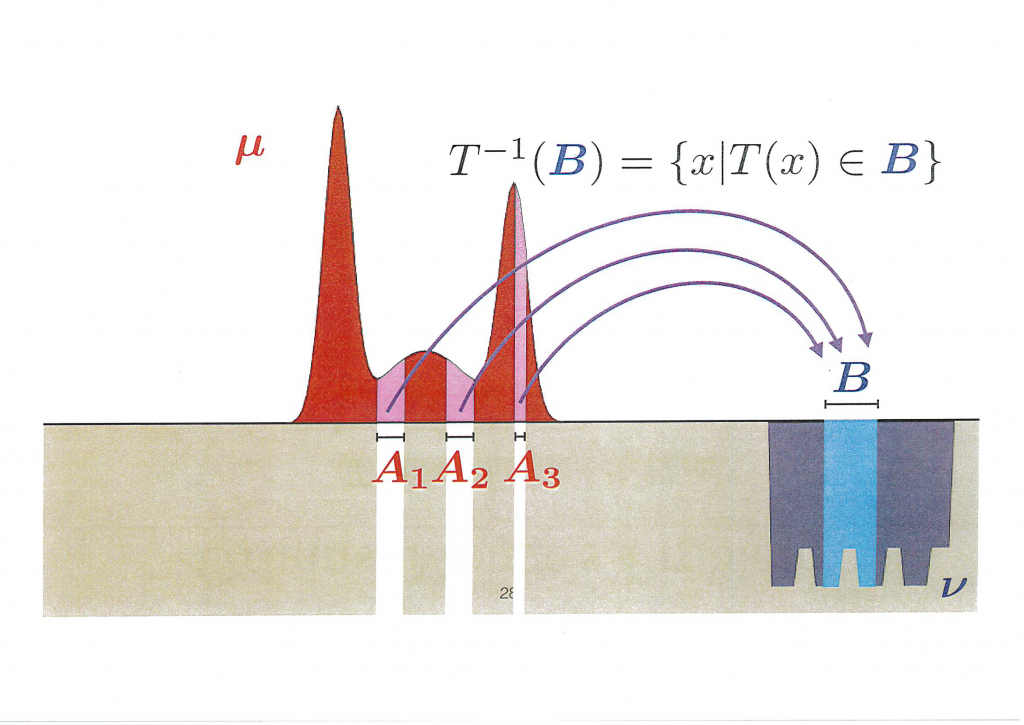
Intuitivement, le travail fourni par l’ouvrier sera proportionnel à la distance D entre les points x et y = T(x). De même, si la masse est importante, le travail à fournir sera également proportionnel au nombre μ de kilos de sable à transporter. Pour l’ouvrier, le « coût » W du déplacement de la pelletée x sera donc μ(x).D(x, T(x)).

Quelles instructions donner à l’ouvrier pour qu’il puisse faire cette allocation ?

En formalisant mathématiquement ceci, si B est une partie du trou à combler, i.e. un segment de l’espace d’arrivée, l’image inverse de B est l’ensemble des x tels que T(x) ϵ B. Ainsi, si selon le plan donné à l’ouvrier, tout le sable amené dans le segment B provient de trois segments A₁, A₂, A₃ du tas de sable, le volume nécessaire pour combler le segment B, de volume ν(B), doit être égal au volume de sable transporté des segments A1, A2, A3. En langage probabiliste, la mesure des trois segments A₁, A₂, A₃ est égale à la mesure du segment objectif B, et ce résultat doit être vrai pour tous les segments B possibles : pour tout B, ν(B) = μ(A₁) + μ(A₂) + μ(A₃).

Ceci signifie que le problème de Monge peut être traduit de la façon suivante : déterminer une application T passant de lieu à lieu, et vérifiant l’égalité ci-dessus pour tout segment B. T est dit envoyer de la masse de lieu à lieu.

Le problème de Monge est très difficile à résoudre, bien qu’il y ait des simplifications possibles. Des progrès récents, autour de 2010, ont été réalisés. J’ai apporté une petite pierre à cet édifice en 2013 (Sinkhorn distances : lightspeed computation of optimal transportation distances), en proposant une technique numérique qui fonctionne bien et permet d’accélérer le calcul du transport optimal. En effet, la question actuelle est comment utiliser la puissance de transport en science des données, comme une fonction de perte, ce qui soulève des questions de calcul importantes. Les deux questions, modèle génératif et transport optimal, sont clairement imbriquées. Ce qu’on essaie de faire actuellement est de calculer le gradient de la distance de Wasserstein par rapport aux paramètres, idée vraiment très récente en statistique théorique, car envisagée en 2006. Sur ce thème, depuis deux ans, de nombreuses publications ont eu lieu, déjà évoquées.

Une application simple de ce qui précède. De la base de données MNIST (Modified National Institute of Standards and Technology, base de données constituée de chiffres écrits à la main, très utilisée en apprentissage automatique) est issue le tableau A. On cherche une fonction à valeurs dans l’espace latent et qui engendre des pixels ; le tableau B en fournit les résultats. L’espace latent est [0,1]² , donc comporte deux coordonnées. Ces deux seules coordonnées sont utilisées pour générer des chiffres et on retrouve pourtant toute la variété de chiffres.

Ces techniques ont été appliquées à de vraies images. On peut engendrer une base d’images de chiens, non pas prises par un appareil photo, mais artificiellement créées par ordinateur.

Au niveau des femmes et hommes, des travaux de recherche récents, à base de modèles génératifs, conduisent à des résultats impressionnants de NVIDIA, société américaine fournisseur de processeurs, cartes et puces graphiques. Même si, comme pour les chiens, tout n’est pas parfait, les douze photos ci-dessus, inimaginables il y a quatre ou cinq ans, montrent des êtres humains qui n’existent pas ; ces visages sont totalement synthétiques et artificiels, obtenus en passant d’une image pas très fine à des images de plus en plus fines avec des techniques d’images modifiées.

Modèles génératifs et transport optimal sont vraiment de beaux exemples réussis de transfert technologique.