Article initialement publié dans Variances n°42 d’octobre 2011. Cet article s’appuie sur le travail réalisé par Clémence Bonniot, Anne Degrave, Guillaume Roussellet et Astrid Tricaud, lors de leur 2ème année à l’ENSAE en 2011, dans le cadre d’un mémoire de statistiques appliquées encadré par Julyan Arbel et Pierre Jacob.
Quand un quidam visite un musée d’art moderne et qu’il observe une œuvre telle que 1024 Colours de Gerhard Richter (Figure 1), il peut naturellement se poser la question suivante : les couleurs ont-elles été choisies une par une, minutieusement, suivant une intention précise de l’auteur, ou ont-elles été placées aléatoirement par un peintre malicieux, riant sous cape en imaginant les critiques chercher un sens là où il n’y aurait que de l’aléatoire ? Dans le cas de cette peinture, la technique est expliquée par le peintre lui-même, qui déclare[1] avoir utilisé un processus aléatoire programmé sur ordinateur pour placer les couleurs, réduisant à dessein le rôle de la volonté de l’artiste dans la création de l’œuvre. Cette peinture fait partie d’une série datant de 1973, Colour Charts, qui compte une cinquantaine de grilles de différentes tailles (de 6 à 5000 couleurs).
![Figure 1: 1024 Colours, 1973, Gerhard Richter [2]](https://variances.eu/wp-content/uploads/2017/02/image1-2.png)
Figure 1: 1024 Colours, 1973, Gerhard Richter [2]
Pour s’attaquer à ces questions d’un point de vue statistique, il s’agit d’abord de transformer ces tableaux en jeux de données. Le site du peintre propose des photographies des peintures, à partir desquelles nous avons opéré une simplification : nous avons extrait de chaque case de la grille une couleur moyenne, représentée par un triplet de nombres correspondant aux composantes « Rouge », « Vert », « Bleu » (modèle RVB). La peinture 1024 Colours devient alors une matrice de taille 32 x 32, contenant des triplets de couleurs. Les données peuvent aussi être représentées de manière équivalente en triplets de « Teinte », « Saturation », « Luminosité » (modèle TSL). Bien entendu, la structure matricielle est importante car la position des cases les unes par rapport aux autres devra être prise en compte. Une fois ce jeu de données constitué, une première étude a été faite sur les couleurs indépendamment de leur disposition.
La répartition des couleurs est-elle uniforme?
Une étape préliminaire pour comprendre les données consiste à tracer les représentations graphiques suivantes: histogrammes, nuages de points… sur un jeu de données aussi coloré, les possibilités de produire de jolis graphes ne manquent pas[3]. On souhaite d’abord répondre à une question simple: la répartition des couleurs sans prendre en compte leur position est-elle uniforme ? Tracer l’histogramme de données tridimensionnelles relève de la gageure. Les histogrammes couleur par couleur pallient cette difficulté et permettent de se donner une première idée. On apprend à ce stade que la distribution de chaque composante diffère nettement d’une loi uniforme, et présente un surplus de valeurs foncées. L’histogramme de la teinte dans le modèle TSL montre que certaines couleurs de l’arc-en-ciel sont sous représentées dans le tableau, à savoir les verts et les violets. Les nuages de points permettent d’apprendre sur l’aspect multivarié des données, c’est-à-dire la corrélation entre les composantes. Par exemple, on représente les points dans les plans constitués de couples de composantes (on observe des points dans les lois marginales bivariées). On constate que la première bissectrice est toujours sur-représentée dans le modèle RVB. Cela est corroboré par le nuage des points dans le cube de la Figure 2: les points se concentrent le long de la diagonale entre le sommet noir et le sommet blanc.
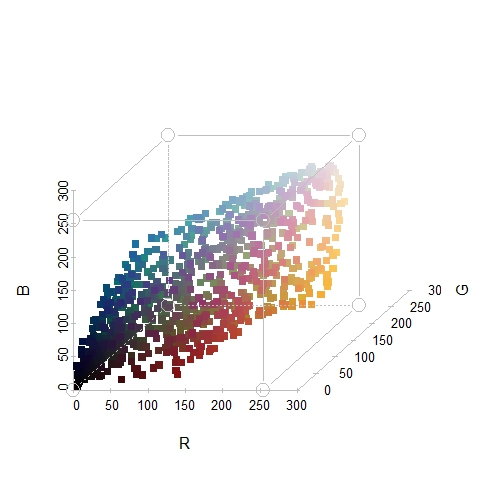
Figure 2: Représentation en perspective des cases selon leurs coordonnées dans le modèle RGB.
De nombreux tests statistiques ont permis de quantifier ces premières intuitions. L’ensemble des résultats montre finalement que les couleurs n’ont vraisemblablement pas été tirées uniformément dans les différents schémas de couleurs considérés. Mais après tout, ce n’est pas exactement ce qu’avait affirmé l’auteur, dont le but était de minimiser le rôle de sa propre volonté dans son procédé artistique.
Y a-t-il des corrélations entre les différentes cases ?
Après ce travail descriptif et afin de répondre à la question initiale, il s’agit de prendre en compte la dimension spatiale des données : il y a des couleurs, et il y a des positions sur la toile. On peut interpréter l’hypothèse d’aléa dans les données comme une hypothèse sur l’autocorrélation spatiale. Ici cette dernière indique si la couleur d’une case donnée « influe » sur les couleurs des cases voisines. Si elle est nulle, cela indique que la couleur d’une case n’a pas d’effet direct sur les couleurs voisines (penser à l’ « effet de neige » que l’on peut observer sur les téléviseurs déréglés). Les cases voisines sont ici définies comme les cases se situant sur les côtés et aux coins d’une case donnée. La Figure 3 montre, pour chaque composante, le niveau de la composante (de rouge) de chaque case en abscisse, et le niveau moyen de la composante (de rouge) sur les cases voisines en ordonnée. La droite de régression qui traverse le graphe permet de détecter s’il y a une tendance positive ou négative. Ici la droite est presque horizontale (pente non significativement différente de 0), indiquant une absence d’effet spatial. Un test (dit de Moran) vient confirmer et quantifier ce constat.
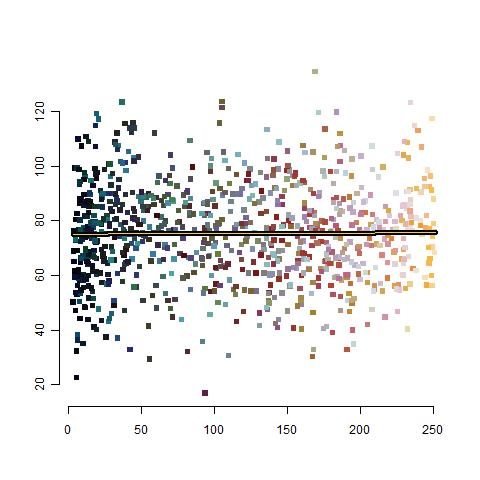
Figure 3: Moyenne des niveaux de rouge des 8 cases voisines en fonction du niveau de rouge (échelle de 0 à 256); droite de régression (d’équation y = 0.002 x + 75).
Malgré l’absence uniformité des couleurs elles-mêmes, on trouve ainsi que les couleurs d’une case ne sont pas corrélées avec les couleurs voisines. En ce sens la méthodologie mise en oeuvre confirme le succès de l’auteur, qui a véritablement construit une série d’œuvres uniques de ce point de vue, où la couleur de chaque partie du tableau est imprévisible, même si l’on connaît les autres parties. Le même test d’autocorrélation spatiale appliqué à la plupart des tableaux (pourvu que l’on s’accorde sur la manière de découper un tableau en cases) donnerait à coup sûr des résultats différents, que l’œuvre soit figurative ou pas.
Appliquer des méthodes statistiques à tout (et n’importe quoi)
Au-delà de l’enjeu, en somme très limité, de l’étude présentée dans cet article, il nous a semblé instructif d’utiliser et de faire utiliser à des élèves des méthodes classiques sur un problème original, voire loufoque. D’une part pour souligner l’aspect universel de la statistique en tant que science, mais aussi en tant que métier: le statisticien peut être amené pendant sa carrière à papillonner entre de nombreux secteurs, comme l’atteste l’annuaire des anciens de l’ENSAE (il y a certes peu d’opportunités de carrière en tant que statisticien critique d’art). Et d’autre part pour souligner les limites de ces méthodes statistiques, qui s’appliquent toujours mais dont il faut savoir bien interpréter le résultat dans le contexte d’application, et le confronter à la question initiale.
[1] Sur son site internet http://www.gerhard-richter.com/
[2] Image tirée de son site, ibid.
[3] Des images qui n’ont pas été reproduites dans cet article sont accessibles en ligne sur le blog Statisfaction: http://statisfaction.wordpress.com/2011/08/09/richter/
- Analyse statistique d’une peinture abstraite - 17 février 2017




![Quelle place pour l’or dans le portefeuille de réserves d’une banque centrale? [1]](https://variances.eu/wp-content/uploads/2019/06/gold-163519_1280-1-440x264.jpg)

Commentaires récents