Les premiers résultats de l’édition 2018 du Programme international pour le suivi des acquis des élèves (PISA) seront publiés cette année par l’Organisation de coopération et de développement économiques (OCDE). Si cette enquête internationale a, au tout début, été accueillie en France avec indifférence voire une certaine défiance, le « classement PISA » a depuis largement intégré le débat public sur l’éducation dans notre pays. La principale source de préoccupation chez nous porte sur l’équité, ou plutôt l’iniquité du système scolaire. Lors des éditions précédentes du PISA, les scores des élèves français étaient proches de la moyenne de l’ensemble des pays de l’OCDE mais le système était jugé comme l’un des plus inégalitaires.
Qu’est-ce que le PISA ?
L’intérêt du PISA dépasse évidemment la production d’un « palmarès ». Rappelons d’abord qu’il constitue la plus grande étude internationale dans le domaine de l’éducation. Administrée tous les trois ans depuis 2000, l’enquête s’est déroulée en 2018 dans près de 80 pays, dont la liste ne se limite plus aux pays de l’OCDE. En France, l’échantillon comprenait environ 7 000 élèves de 15 ans, appartenant à environ 250 établissements scolaires – mais dans l’ensemble des pays participants, c’est plus d’un million d’élèves de cet âge qui a été interrogé.
L’une des originalités du PISA tient à ce qu’il ne se contente pas de mesurer des connaissances scolaires, mais vise à évaluer la capacité des élèves à mobiliser ces acquis scolaires dans des contextes variés. L’enquête se concentre sur plusieurs domaines clés – la compréhension de l’écrit, la culture scientifique et mathématique auxquels s’ajoute, à chaque édition, un domaine novateur comme, en 2015, la capacité à résoudre des problèmes de manière collaborative. Ce qui est mesuré, plutôt qu’une simple restitution de connaissances scolaires, se rapporte à la notion de « littératie » (litteracy), c’est-à-dire la capacité d’exploiter des savoirs et savoir-faire [1]. Les exercices proposés aux élèves sont donc ancrés dans des situations concrètes de la vie quotidienne ou interrogent leur culture scientifique ou mathématique. Les résultats des exercices conduisent à donner un « score » à chaque élève, en utilisant un modèle statistique dit de « modèle de réponse à l’item » (ou Item Response Theory, IRT) [2]. Ce modèle, proposé initialement par le statisticien Raoul Rasch, consiste à inférer le niveau (inobservé) de l’élève en fonction du nombre de réponses correctes que l’élève a obtenues, en tenant compte de la difficulté des exercices. La complexité des exercices est elle-même estimée simultanément en fonction du nombre d’élèves qui sont parvenus à les résoudre. Ces modèles permettent également de tester que les items « fonctionnent » de manière identique dans tous les pays – dit autrement, que le niveau de difficulté des exercices perçu n’est pas lié à des raisons linguistiques ou culturelles, de manière à assurer la comparabilité des scores obtenus entre élèves de pays différents [3].
L’objectif du programme est aussi de cerner les facteurs qui influent sur l’acquisition des connaissances et des compétences et le développement des attitudes à l’école et dans le milieu familial, afin d’étudier leurs interactions et leurs implications pour l’action publique. Le PISA permet en effet de mettre en relation les résultats des élèves avec un ensemble de variables contextuelles. Les tests cognitifs sont complétés par plusieurs questionnaires renseignés par les élèves ainsi que par les principaux des établissements dans lesquels ils sont scolarisés. L’enquête interroge les élèves sur leur milieu familial (niveau d’éducation et métiers de leurs parents, possession de biens culturels, etc.). Il est donc possible de mettre en relation les niveaux de performances des élèves avec des informations sur leur milieu social, les caractéristiques des écoles qu’ils fréquentent ou encore les spécificités du système scolaire (usage du redoublement, préscolarisation précoce, etc.).
Ce sont ces informations qui permettent d’estimer les indicateurs relatifs à l’équité. Les publications de l’OCDE appréhendent cette notion complexe – que l’édition française traduit souvent par égalité – via deux dimensions complémentaires : « l’inclusion » et la « justice ».
Un système équitable : inclusif et offrant des chances égales à toutes et tous
L’inclusion renvoie à l’objectif de « faire en sorte que tous les élèves acquièrent des compétences fondamentales essentielles pour participer pleinement à la vie de la société » [4]. Il s’agit donc de mesurer un niveau de performance minimal censé attester de la maitrise de compétences élémentaires nécessaires à une insertion réussie dans la vie d’adulte. En 2015, 22 % des élèves français ne maitrisaient pas un niveau « suffisant » en science, soit légèrement plus que la moyenne de l’OCDE (19 %). Dans une acception plus littérale, l’inclusion est aussi définie comme la possibilité donnée à tous les élèves d’étudier ensemble ou, son contraire, par la sélection dans certaines écoles en fonction du niveau scolaire ou de l’origine sociale. Les indicateurs statistiques correspondants sont estimés à partir de la distribution, plus ou moins uniforme, des élèves dans les écoles.
La deuxième dimension de l’équité mesurée dans PISA, la justice, se rattache plutôt au courant de philosophie politique développé par John Rawls, qu’on peut parfois traduire sous le terme d’égalité des chances. Il s’agit non de viser à ce que toutes et tous parviennent aux mêmes résultats, mais d’assurer que les inégalités de score observées entre les élèves ne relèvent pas de « circonstances » individuelles. Ces circonstances correspondent à des facteurs sur lesquels les élèves n’ont aucune prise, notamment leur sexe, leur milieu social ou leur statut au regard de l’immigration. Dans les publications PISA, on définit ainsi que « les systèmes d’éducation sont égalitaires s’ils offrent à tous les élèves, quel que soit leur milieu, autant de possibilités de réussir à l’école » [5]. En particulier, le « gradient socio-économique » dans PISA mesure la force du lien entre le score obtenu et un indicateur composite mesurant le niveau d’éducation des parents, leurs professions ainsi que des indicatrices de ressources financières et culturelles du foyer, l’indice de statut économique, social et culturel (SESC). En pratique, ce gradient est simplement mesuré par une régression linéaire du score individuel des élèves sur l’indicateur approchant leur milieu social. La force du gradient socio-économique correspond à la part de la variance du score dans PISA expliquée par l’origine sociale (le R2).
Ainsi, en France, l’origine sociale ainsi calculée expliquait 20 % du score individuel dans PISA en 2015, soit le plus haut niveau observé dans les pays de l’OCDE (pour lesquels la moyenne s’établit à 13 %). La pente du gradient social correspond au coefficient de cette même régression : il capte donc l’amplitude des inégalités de score moyennes entre des élèves d’origine sociale différente. Un autre indicateur de l’égalité – ou de l’inégalité – des chances est fourni par le rapport des risques entre deux sous-populations définies par des caractéristiques individuelles. Comme illustré dans le graphique ci-dessous, les élèves défavorisés (définis dans PISA comme ceux dont l’indice SECS est inférieur au premier quartile de la distribution de cet indice dans leur pays) avaient ainsi en France quatre fois plus de risque que des élèves plus favorisés de ne pas atteindre le niveau des compétences de base en science en 2015, soit le ratio le plus élevé des pays de l’OCDE.
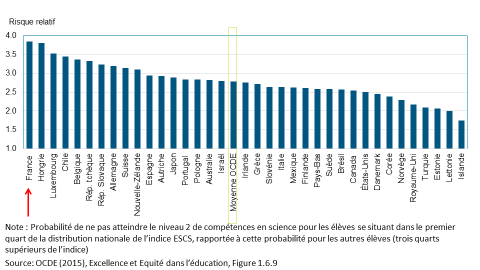
Graphique : Risque relatif entre élèves issus de milieu défavorisé et élèves plus favorisés de ne pas atteindre le niveau de compétences de base en science dans PISA en 2015
De la description à la prescription
Le PISA permet de mettre en relation politiques éducatives et pratiques (sélection précoce, usage plus ou moins intensif du redoublement, etc.) et résultats des élèves. Bien que la tentation soit souvent forte d’expliquer les bons résultats observés dans tel système scolaire par certaines de ces caractéristiques, extrapoler des relations causales à partir de simples corrélations entre les caractéristiques des système scolaires et leurs scores dans PISA est hasardeux. Par exemple, dans de nombreux pays, il est fréquent d’alléger les effectifs des classes rassemblant de nombreux élèves en difficultés. De ce fait, on observe généralement une corrélation positive entre le nombre d’élèves d’une classe et son niveau scolaire. Il serait néanmoins hasardeux d’en conclure qu’une politique éducative efficace consisterait à augmenter la taille des classes. Plus généralement, chaque système éducatif a de nombreuses spécificités et il est impossible d’isoler celui qui pourrait expliquer la réussite de ses élèves. Peut-on expliquer la réussite du « modèle finlandais », qui occupe régulièrement les premières places du « podium » dans PISA par la formation et la sélection des enseignants, la faible sélection, l’âge tardif de la scolarité obligatoire, la plus ou moins grande autonomie des établissements, la taille des classes… ou une combinaison de tout cela ? Toutes ces dimensions sont mesurées en même temps dans un cycle de PISA, et il sera très complexe par des comparaisons internationales « en coupe transversale » d’identifier celui qui fait vraiment la différence.
L’intérêt de PISA est cependant de montrer en quoi les systèmes d’éducation se ressemblent et se différencient, et de mettre en perspective les résultats des uns avec les pratiques des autres. À rebours des fausses évidences, il a par exemple permis de montrer que les systèmes qui pratiquaient une sélection précoce dans des voies d’enseignement différencié (comme l’Allemagne ou l’Autriche) s’avéraient à la fois moins performants et plus inéquitables, quand certains systèmes « inclusifs », dans lesquels les élèves poursuivent très longtemps une scolarité commune, affichaient d’insolents bons résultats (la Finlande étant l’exemple le plus cité). De fait, l’un des enseignements récurrents du PISA, observé sur l’ensemble des cycles passés, est que l’excellence d’un système scolaire ne se fait pas nécessairement au détriment de l’équité. De nombreux pays, dont les scores sont les plus élevés dans PISA, sont parvenus à réduire le poids de l’origine sociale dans la réussite, à dégager une élite performante et à minimiser la part des jeunes ne maitrisant pas les compétences de bases, comme illustré dans le graphique suivant. L’OCDE publiera en décembre de cette année des mesures de l’enquête 2018 qui montreront si le système scolaire français est parvenu à progresser vers ces objectifs.
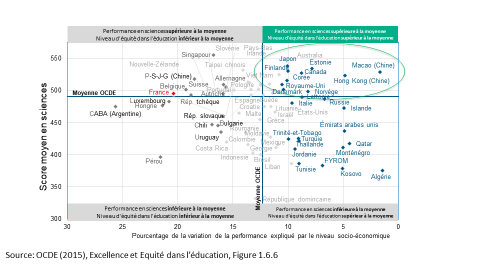
Graphique : Performance et équité dans PISA en 2015
Pauline Givord, après avoir dirigé une unité du département des études économiques et lancé le SSP Lab [6] au sein de l’Insee, est actuellement analyste au sein de la direction de l’Éducation de l’OCDE, responsable des travaux sur l’équité dans l’enquête PISA 2018.
Mots clés : PISA – équité dans l’éducation – égalité des chances – évaluation des systèmes éducatifs – mesure des compétences
[1] On trouvera des exemples d’exercices ainsi qu’une documentation plus complète de l’enquête sur le site PISA de l’OCDE : https://www.oecd.org/pisa/test-fr/ (édition 2012) ou https://www.oecd.org/pisa/test/ (édition 2015).
[2] Pour une présentation pédagogique de ces méthodes, voir par exemple Rocher (2015), « Méthodes psychométriques utilisées dans le cadre des évaluations des élèves », Education et Formation n°86-87.
[3]Voir encore Rocher (Ibid.) ou pour une présentation plus précise du traitement de ces items dans PISA le PISA 2015 Technical Report (https://www.oecd.org/pisa/data/2015-technical-report/), notamment les chapitres 9 et 12.
[4] OCDE (2016), Résultats du PISA 2015 (Volume I), L’excellence et l’équité dans l’éducation.
[5] Ibid.
[6] Le SSP Lab est un centre de ressources et d’animation pour la recherche appliquée et le développement expérimental visant à promouvoir l’innovation et la nouveauté en matière de sources de données, de technologies et de méthodes de data science, relatives aux productions statistiques du système de statistique publique (SSP).
- Comment mesure-t-on l’équité d’un système éducatif ? - 22 mai 2019


Commentaires récents