Publié sur le compte Linkedin de l’auteur le 13 mars 2017 – Avec l’aimable autorisation de l’auteur
Luis Enrique, le coach de Barcelone, n’est pas seulement un grand entraîneur : c’est un expert en statistiques. Et s’il a administré au PSG une leçon de football, il nous a offert par la même occasion trois leçons de probabilités. (Pour ceux qui ne suivraient pas l’actualité du football, rappelons que, en 8èmes de finale de la Ligue des Champions, le PSG a été battu 6-1 à Barcelone le 8 mars après avoir gagné 4-0 à Paris le 14 février).
De la débâcle du PSG au Camp Nou, on peut tirer toutes les leçons de leadership et de management des hommes. Et la presse ne s’en prive pas. Mais il peut être amusant d’y voir aussi un bel exemple de prévision probabiliste. On se souvient que Luis Enrique, l’entraîneur de Barcelone, a eu, la veille du match, des propos prémonitoires : « S’ils en ont marqué quatre, on peut en mettre six ». Ce qui passait pour une rodomontade annonçait en fait la remontada.
Alors, Enrique est-il voyant ? Sans doute son optimisme est-il communicatif, et contribue-t-il puissamment au triomphe de son équipe. Mais il démontre aussi une parfaite maîtrise du théorème de Bayes – un outil essentiel à toute prévision dans un environnement incertain.
Leçon 1 : connaître la probabilité a priori
Pour le comprendre, il faut d’abord réaliser que nos estimations de la probabilité d’un événement ne dépendent pas seulement des faits que nous observons, mais aussi de ce que nous pensons être leur probabilité a priori. Supposez par exemple que vous observiez un skieur qui descend une piste difficile sans tomber, trois fois de suite. Quelle est, à votre avis, la probabilité qu’il y parvienne une quatrième fois ? Elevée, sans doute. Mais si vous saviez au départ que ce skieur est un moniteur, votre estimation de cette probabilité sera plus élevée encore. A priori, avant toute observation des trois descentes, vous créditez le moniteur d’une probabilité de succès plus grande qu’un skieur moyen. Et vous avez bien raison : la probabilité a posteriori dépend de l’observation, mais aussi de la probabilité a priori.
Le théorème de Bayes permet de quantifier cette intuition, en calculant la probabilité a posteriori à partir de (1) la probabilité a priori, et de deux probabilités distinctes concernant l’observation nouvelle : les probabilités que cette observation se produise si (2) l’hypothèse est vraie et (3) l’hypothèse est fausse. (La formule est en bas de l’article, pour les amateurs, avec en Annexe 2 les calculs correspondant à tous les exemples qui suivent.)
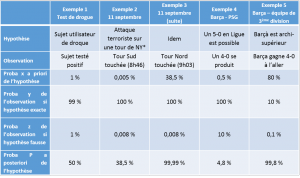
Pour illustrer l’importance de ce calcul, prenons l’exemple d’un test qui dépiste les utilisateurs d’une drogue illicite. Supposons que ce test soit fiable à 99% dans les deux sens, c’est-à-dire que 99% des utilisateurs de drogue sont détectés et que 99% des verdicts positifs révèlent effectivement un utilisateur de drogue. En d ‘autres termes, il n’y a que 1% de « faux négatifs » et 1% de « faux positifs ». Ces chiffres semblent indiquer un test presque infaillible : intuitivement, ils nous suggèrent qu’un test positif révèle effectivement un coupable dans 99% des cas.
Pourtant, la réalité est très éloignée de ce chiffre – du moins, si l’usage de la drogue en question est peu répandu. Supposons par exemple que la population comprenne 1% d’utilisateurs de la drogue en question. Avant tout test, la probabilité a priori qu’un individu soit un utilisateur est de 1%. Sachant qu’un individu est testé positif, quelle est la probabilité qu’il soit effectivement consommateur ? Faites le calcul (exemple 1 en Annexe 2) : dans ce cas, à peine une chance sur deux ! Stupéfiant (c’est le cas de le dire), mais compréhensible quand on le représente de la manière suivante en partant d’une population de 10.000 personnes :
Population totale : 10000 => 100 utilisateurs (1 %) et 9900 non utilisateurs (99%)
Parmi les 100 utilisateurs, il y en a 99 (99 %) détectés à raison et 1 non détecté à tort (1 %).
Parmi les 9900 non utilisateurs, 99 (1%) sont détectés à tort et 9801 sont non détectés à raison.
Il y a donc 99 détectés à raison parmi les utilisateurs et 99 détectés à tort parmi les non utilisateurs, c’est-à-dire que la moitié des tests positifs est due à des non utilisateurs.
Leçon 2 : réviser sa probabilité en fonction des événements
Mais quel rapport avec Luis Enrique, vous demandez-vous ? Venons-y. Tout l’intérêt de cette formulation du théorème de Bayes, c’est qu’elle nous permet de réviser notre estimation a priori de la probabilité d’un événement à la lumière de faits nouveaux. Et on peut en tirer ce résultat général : une fois qu’un événement improbable s’est produit, la probabilité qu’il se reproduise augmente.
Dit comme ça, cela semble à la fois contre-intuitif et évident. Contre-intuitif : si j’ai gagné au loto, je ne m’attends pas à regagner la semaine prochaine. Et pourtant évident, comme le montre cet exemple emprunté à Nate Silver*: a priori, le 10 septembre 2001, la probabilité d’une attaque terroriste utilisant un avion sur une tour new-yorkaise est infime, car la chose ne s’est jamais produite. Le 11 septembre à 8h46, après la première attaque, cette probabilité doit être révisée à la hausse, mais l’idée que le premier impact puisse n’être qu’un accident est encore crédible. A 9h03, après l’attaque sur la Tour Sud, la probabilité que la collision soit une attaque terroriste, et non un accident, est une quasi-certitude. C’est parce que l’hyper-improbable s’est produit qu’il devient moins improbable. (Calculs en Annexe 2, exemples 2 et 3).
Le raisonnement est à peu près le même pour Luis Enrique. L’hypothèse est ici qu’un match de Ligue des Champions peut se solder par un score de 5 buts d’écart. Quelle est la probabilité que cette hypothèse soit vraie ? A priori – soit avant le match aller –, très faible. Le HuffPost nous apprend qu’un score de 4-0 était coté à 100 contre 1 chez les bookmakers avant le match aller, et qu’un tel score n’avait jamais été remonté par une équipe en compétition européenne depuis 60 ans. On peut donc dire que la probabilité a priori d’un 5-0 était bien inférieure à 1% — disons, par hypothèse, de 0,5%.
Seulement voilà : le 14 février, le PSG gagne 4-0. Que nous apprend cet événement sur la possibilité d’une victoire 5-0 ? La première partie de la question est facile : si un 5-0 est possible, alors un 4-0 l’est évidemment aussi. Donc la probabilité de l’observation si l’hypothèse est exacte est de 100%.
Il est plus difficile d’estimer la probabilité de l’observation si l’hypothèse est fausse, c’est-à-dire qu’un 4-0 soit possible mais un 5-0 impossible. L’affirmation de Luis Enrique n’est pas mécaniquement exacte : ce n’est pas parce que les parisiens ont marqué 4 buts que les catalans peuvent en mettre six (ni même cinq). En théorie, 4-0 peut être un score « possible mais indépassable ». Quelle probabilité assigner à cette hypothèse ? Evidemment, on n’en sait rien, mais on peut faire varier le chiffre et tester la sensibilité du résultat.
Et celui-ci est fort intéressant. Si on pense (comme Luis Enrique, manifestement) que si un 4-0 est possible, alors il y a 90% de chances qu’un 5-0 le soit, la probabilité que nous devons utiliser est de 10%. Bayes nous permet de calculer la probabilité du 5-0 : 4,8% (exemple 4 de l’Annexe 2). C’est faible dans l’absolu, bien sûr, mais c’est dix fois plus qu’avant le match aller ! Cette probabilité n’est d’ailleurs pas très loin de la cote de 12 contre 1 que les bookmakers assignaient à la remontada. (Si l’on est beaucoup plus prudent et qu’on estime qu’il y a 25% de chances qu’un 5-0 demeure impossible même après le constat d’un 4-0, alors le résultat est 2% : plus faible encore, mais toujours quatre fois plus qu’avant.)
En somme, Luis Enrique est un parfait bayésien, qui révise sa probabilité a priori en fonction des événements… et qui prouve la justesse de son calcul sur le terrain.
Leçon 3 : choisir le bon échantillon
Encore faut-il remarquer que Luis Enrique choisit de regarder le problème sous un angle bien particulier. Beaucoup d’experts disaient en effet simplement que remonter un 4-0 était impossible, puisque ça ne s’était jamais produit.
Pourquoi Luis Enrique ne suit-il pas ce raisonnement ?
La raison est simple. Supposons que le Barça gagne 4-0 un match aller contre une équipe notoirement plus faible — par exemple, Gijon ou Valladolid, pour faire plaisir au commentateur de Canal qui, à la 84ème minute du match, triomphait : « c’est pas Gijon, c’est pas Valladolid, c’est le PSG ! ». Enrique n’en conclura bien sûr pas qu’une défaite 5-0 est possible au retour, mais au contraire qu’une nouvelle victoire de Barcelone est probable. Son raisonnement est toujours bayésien, mais centré sur une hypothèse bien différente : il part de l’hypothèse a priori que le Barça est largement supérieur à cette équipe médiocre, et la battra à chaque match. Une victoire écrasante n’est que modérément probable si cette hypothèse est juste (on ne fait pas 4-0 tous les soirs), mais elle est infiniment improbable si l’hypothèse est fausse (on ne met quasiment jamais 4-0 à une équipe supérieure). Le 4-0 du match aller augmente donc la conviction qu’a l’entraîneur de la supériorité de son équipe : de très probable a priori, celle-ci devient a posteriori quasi-certaine. (Chiffres en Annexe 2).
L’intérêt de ce contre-exemple est de nous révéler la différence entre le raisonnement bayésien subtil de Luis Enrique et la statistique simpliste de ceux qui disaient : « ça n’est jamais arrivé, donc c’est impossible ». Quand les historiens du foot observent que l’on n’a jamais remonté un 4-0, ils regardent des 4-0 où une équipe médiocre s’est faite « dérouiller » par des champions. Dans un tel cas, le 4-0 rend bien une nouvelle défaite plus probable. Mais Luis Enrique part du principe que le PSG et le Barça sont deux grandes équipes de niveau comparable, et que quand elles s’affrontent, tout peut arriver ! Pour lui, ce que révèle le 4-0 du Parc des Princes, ce n’est pas un écart de niveau, c’est un accident du destin. Et Bayes nous le dit : la survenance d’un accident du destin rend plus probable un autre accident du même genre, éventuellement en sens inverse.
Seule consolation pour le PSG, le raisonnement d’Enrique démontre qu’il est tout à fait d’accord avec Stéphane Guy : le PSG, ce n’est pas Gijon, ni Valladolid, mais une grande équipe de niveau finalement assez équivalent à celui de Barcelone. Il lui fait donc, par Bayes interposé, un grand compliment ! Sans doute est-ce là le seul éloge que ce match aura valu aux malheureux parisiens…
Annexe 1 : La formule de thomas Bayes
Le théorème du pasteur et mathématicien britannique (1702-1761) permet de calculer des probabilités conditionnelles. Vous vous rappelez peut-être avoir appris comment calculer la probabilité de « A sachant B » à partir des probabilités de A, B, et « B sachant A ». La formulation du théorème qui nous intéresse ici est une permutation de la formule, qui permet de réviser la probabilité qu’une hypothèse soit exacte à la lumière d’une observation nouvelle :
P = xy / (xy+ z(1-x))
où :
x est la probabilité a priori que l’hypothèse soit exacte ;
y est la probabilité de l’observation si l’hypothèse est exacte ;
z est la probabilité de l’observation si l’hypothèse est fausse.
Annexe 2 : Les exemples de ce post
Le tableau ci-dessous illustre (avec des valeurs évidemment discutables) les calculs qui sous-tendent les exemples mentionnés ci-dessus.
(*) : Exemple emprunté à Nate Silver, « The signal and the noise : Why So Many Predictions Fail – But Some Don’t », 2012, Penguin Group
La probabilité z que l’impact soit un accident est calculée à partir de l’historique des accidents d’avion






Commentaires récents