Claude Shannon, SIGSALY et les communications secrètes : un hommage pour le centenaire de sa naissance

Cet article a été publié dans la revue de l’ARCSI. L’ARCSI est un réseau de compétences en matière de cryptologie et de cyber-sécurité, riche patrimoine de matériels et de documents qui fêtera ses 90 ans en 2018.

« Nous connaissons le passé, mais nous ne pouvons pas le contrôler. Nous contrôlons l’avenir, mais nous ne pouvons pas le connaître. » – C.E. Shannon

Introduction

La science de l’information est née il y a 79 ans, avec les travaux d’un homme exceptionnel : Claude Elwood Shannon (30 avril 1916 – 24 février 2001). Nous avons célébré l’an dernier le centenaire de sa naissance. Mathématicien et ingénieur, il a fait émerger la science de l’information et a développé la théorie des communications secrètes dans les années 1940. Shannon a fait passer la cryptographie d’un art à une science.

Shannon a participé au projet Top Secret SIGSALY des Bell Telephone Laboratories (BTL), l’équipement de cryptophonie utilisé par Roosevelt et Churchill pendant la Deuxième Guerre mondiale. Il s’est passionné pour la cryptologie, la science de la parole et pour toutes les recherches associées. Dans un document historique de l’année 1948, Shannon a fourni une définition mathématique de l’information et d’une transmission chiffrée sur canal bruyant. L’œuvre de Shannon a unifié, en une seule théorie, tout le domaine des télécommunications : le télégraphe, le téléphone, la radio et la télévision. Ses travaux constituent la base de notre monde numérique moderne.

Shannon est né à Petoskey dans le Michigan (États-Unis). Dès ses premières années, il a montré un vif intérêt pour les équipements mécaniques et électriques. Le héros de son enfance était Thomas Edison dont il était un cousin éloigné !

Pendant ses études secondaires, les sciences et les mathématiques furent ses matières préférées.

Durant sa jeunesse, Shannon a construit des maquettes d’avions, une maquette de bateau radiocommandé et un système de télégraphe qui utilisait 800 m de fil de clôture pour communiquer avec un ami. Il a au passage travaillé comme messager à la Western Union Telegraph.

Un étudiant brillant

En 1936, Shannon obtient sa licence (Bachelor’s Degrees) en ingénierie électrique et en mathématiques de l’Université du Michigan. Il poursuit ses études supérieures au M.I.T. (Massachusetts Institute of Technology) sur un analyseur différentiel mécanique sous la responsabilité de Vannevar Bush un grand pionnier de l’informatique.

À l’âge de 22 ans, Shannon obtient sa maîtrise (Master’s Thesis) au M.I.T. son mémoire est intitulé : A Symbolic Analysis of Relay and Switching Circuits. Sa thèse est publiée, en 1937, dans le prestigieux Journal of the American Institute of Electrical Engineer.

Il s’agissait d’une approche révolutionnaire, utilisant l’algèbre de Boole, de l’analyse et de la synthèse des systèmes à base de relais pour la commutation téléphonique. Il est impressionnant de constater que tous les dispositifs modernes – ordinateurs, téléphones portables, circuits logiques et électroniques – s’appuient sur la thèse de Shannon.

Shannon obtient son doctorat (Ph.D.) en mathématiques au M.I.T. en 1940. Après son doctorat, le voilà chercheur au célèbre Institute for Advanced Study de Princeton. Il a rejoint les BTL en 1940, et y travaillera jusqu’en 1972. Il sera également membre du Research Electronics Laboratory du M.I.T. de 1956 à 1978.

Shannon était toujours un amateur de gadgets : « Je me demandais simplement comment les choses peuvent être mises ensemble ». Génie quelque peu excentrique, il traversait les salles de M.I.T. sur un monocycle ou s’amusait à jongler. En 1949, Shannon épouse Betty (Elizabeth Moore), ils eurent trois enfants : Robert, Andrew et Margarita.

Le téléphone et le monde de la défense

En 1940, Shannon est stagiaire aux BTL au sein du département de recherche en mathématiques. Il y étudie la théorie de la commutation téléphonique. En 1941, il travaille pour la Défense des États-Unis, toujours aux BTL, sur des systèmes de commande de tir et sur la cryptographie. Son travail sur les directeurs antiaériens est devenu crucial lorsque les bombardiers et les missiles allemands attaquèrent Londres pendant le blitz. Il a découvert la formule de gain topologique tout en étudiant le fonctionnement d’un ordinateur analogique pour la commande de tir des pièces d’artillerie.

Avec Harry Nyquist et Homer Dudley, Shannon se penche sur la théorie de la cryptologie et les circuits du système de cryptophonie SIGSALY. En 1942, Shannon invente des graphes de flot pour le signal. En 1944, il écrit un article sur le codage PCM (Pulse-code modulation) pour les téléphones et conçoit un convertisseur analogique-numérique à équilibrage de charge. En 1948, son travail permet d’aboutir au célèbre document, A Mathematical Theory of Communication, publié en deux parties dans le Bell System Technical Journal, puis rassemblées dans un livre en 1949.

Durant les années quarante, le travail de Shannon sur SIGSALY consiste à concevoir le système dans son principe théorique puis les schémas de réalisation. En 1950, Shannon s’est intéressé à la programmation d’un ordinateur destiné à jouer aux échecs. En appliquant la théorie de l’information, avec Edward Thorphe, il invente un moyen de gagner au black jack à Las Vegas, la désormais célèbre méthode High-Low ou Card Counting. Il est aussi le co-inventeur du premier ordinateur transportable permettant d’améliorer les chances de gagner au jeu de la roulette.

En 1952, Shannon construit une souris robot nommée Thesus qui apprend à courir dans des labyrinthes modifiables de 5 x 5 éléments avec des commutateurs et des relais. Il invente également un ordinateur, THROBAC (THrifty ROman-numeral BAckward-looking Computer) calculant en chiffres romains ! Il conçoit en 1961 le Minivac 601, un ordinateur professionnel.

Son crépuscule

Malheureusement, dans les années 1990, Shannon développe la maladie d’Alzheimer, avec une perte progressive des liens cognitifs de son cerveau. Appliquant sa théorie de l’information, Shannon aurait pu dire que toutes les tentatives possibles de correction d’erreur échouant, qu’aucun signal significatif ne pouvant passer, en conséquence la bande passante tombe à zéro… Claude E. Shannon est décédé le 24 février 2001, à l’âge de 84 ans.

Théorie de l’information

En 1948, le papier de Shannon A Mathematical Theory of Communication, se focalise sur la meilleure façon de coder l’information qu’un expéditeur souhaite transmettre. Dans cet ouvrage fondamental, il utilise les outils de la théorie des probabilités, développés par Norbert Wiener.

Ce document lui a servi de fondement à la théorie de l’information. Shannon y a défini mathématiquement la notion d’information pour les ingénieurs des télécommunications ainsi qu’un moyen précis de la quantifier : l’élément binaire autrement dit le bit. Il a développé la notion d’entropie de l’information d’un message comme mesure de l’incertitude, inventant ainsi l’essence même de la théorie de l’information. Shannon a montré comment les données pouvaient être « compressées » et comment obtenir une transmission sans erreur.

La contribution fondamentale de Shannon au traitement des langues naturelles et de la linguistique a été poursuivie dans
son article, Prediction and Entropy of Printed English. En 1951, Shannon a calculé les limites supérieure et inférieure de l’entropie sur les statistiques de l’Anglais, ouvrant la voie à l’analyse statistique des langages. Shannon a prouvé que considérer les espaces comme la 27e lettre de l’alphabet abaisse l’incertitude dans les langues écrites, fournissant un lien quantifiable clair entre la pratique culturelle et la cognition probabiliste.

Shannon a présenté la théorie de l’échantillonnage c’est-à-dire la représentation d’un signal continu par un ensemble discret uniforme d’échantillons. Cette théorie est essentielle dans les télécommunications et a joué un rôle décisif dans la numérisation des transmissions à partir des années 1960, mais aussi de tous les médias.

Bits, correction d’erreur et quantification de l’information

Shannon a défini la quantité d’information produite par une source dans une formule analogue à l’entropie thermodynamique. Il a également analysé la capacité d’envoyer des informations par le biais d’un canal de communication. Il a montré qu’existe un débit maximum c’est-à-dire la bande passante du canal (voir ci-dessous). Il relie la vitesse en bauds au rapport signal/bruit et à la bande passante. Shannon définit l’entropie de l’information comme le nombre de chiffres binaires requis pour coder un message. En 1948, cette numérisation de l’information était une approche révolutionnaire. C’est dans ce papier que Shannon introduit le mot bit ou chiffre binaire.

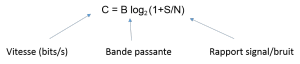
Shannon a démontré mathématiquement qu’une communication parfaite, sans erreur et dans un canal bruyant, exige que le taux de transmission soit au sein de la bande passante du canal et que les codes de correction d’erreurs sont nécessaires pour restaurer les données du signal brouillé. L’électronique moderne d’aujourd’hui, allant des codecs audio et vidéo, aux mobiles et au cinéma Blu-Ray, s’appuie sur les théories mathématiques de Shannon et les corrections d’erreurs.

Claude Shannon et SIGSALY

Aux BTL de New York, Shannon a participé avec Harry Nyquist et Homer Dudley (l’inventeur du VOCODER), à la conception de SIGSALY. Parmi ses nombreuses innovations figurent la modulation par impulsions codées et la définition du bit d’information.

Son équation pour l’information est : h(p) = -log_b (p). Shannon a posé la question : « Qu’est-ce que la base b ? c’est une unité d’information qui représente un choix entre deux possibilités égales » Supposons deux symboles, S1 et S2, avec une probabilité de 50 % chacun.

P = 0,5 et h = -log_b (0,5) = log_b (2) = 1, donc b = 2. L’unité d’information de Shannon est le bit !

Shannon a mis en évidence la dualité entre système de transmission et système de protection de l’information : l’analyse des lignes téléphoniques bruyantes et des messages codés ont la même formulation mathématique. L’objectif d’un système de transmission est de réduire l’entropie et de garantir une récupération précise des informations transmises. L’objectif d’un système de protection de l’information est d’augmenter l’entropie de l’information transmise, tout en permettant sa récupération à l’aide d’une clé unique.

Shannon a démontré mathématiquement que SIGSALY est un système de chiffrement incassable. Cela a conduit à son article de référence The Communication Theory of Secrecy Systems. Par la suite, Shannon a brièvement rencontré Alan Turing aux BTL, mais ils n’ont pas pu discuter de SIGSALY en raison de la classification du sujet.

En 1945, le rapport technique du comité de recherche sur la défense nationale (National Defense Research Committee) sur les commandes de tir comprenait un article intitulé Data Smoothing and Prediction in Fire-Control Systems, par Shannon, Blackman et Bode. Ce papier quantifie le problème du lissage des données dans les commandes de tir analogiques c’est-à-dire « le problème de la séparation du signal du bruit parasite dans les systèmes de communications ». Il a ainsi modélisé le problème en termes de données et de traitement du signal.

Shannon et la cryptographie, la preuve du secret parfait

En 1940, Shannon exprime sa version du principe de Kerckhoff, connue sous le nom de « Maxime de Shannon » : « L’ennemi connaît le système ». En septembre 1945, il écrit un mémoire classifié intitulé Communication Theory of Secrecy Systems, où il prouve que tous les systèmes de chiffrement théoriquement incassables doivent avoir les mêmes exigences qu’une clé aléatoire une fois. Il s’agit du système de chiffrement de Vernam autrement appelé à masque jetable chiffrant le message avec une vraie clé aléatoire. Shannon a montré que la clé aléatoire doit avoir la même longueur que le message. Shannon a prouvé avec rigueur que cette méthode de chiffrement est inviolable. À ce jour, il n’existe aucun autre système de chiffrement réputé incassable. Une version déclassifiée de cet article a été publiée en 1949 dans le Bell System Technical Journal.

Shannon a déclaré que ses idées, durant la guerre, sur la théorie de la communication et la cryptographie se sont développées simultanément et qu’« elles sont si proches, qu’on ne peut les séparer ». Dans une note de bas de page au début du rapport classifié, Shannon annonce son intention de « développer ces résultats… dans un prochain mémorandum sur la transmission de l’information ». Ainsi, les travaux de Shannon sur SIGSALY, l’ont amené à écrire ses deux documents de recherche les plus fondamentaux !

Conclusion

Les importants travaux de Shannon sur les communications modernes, la cryptologie et la théorie de l’information ont eu un impact universel. Son flot ininterrompu de nouvelles théories, de démonstrations, de documents et de réalisations matérielles a duré de 1937 jusqu’aux années 1980. Sans la contribution cruciale de Claude Shannon à la science de l’information, il serait difficile d’imaginer l’existence des médias numériques, des communications ou de l’Internet d’aujourd’hui.

L’influence de Claude Elwood Shannon se perpétue, car ce génie a créé les bases des technologies de l’information et de la communication qui interconnectent notre monde moderne.